Problem C. 1486. (May 2018)

C. 1486. A regular triangle \(\displaystyle ABC\) and a circle \(\displaystyle k\) are both centred at point \(\displaystyle O\), and have an equal area of \(\displaystyle \sqrt{\frac{\pi}{\sqrt{27}}}\). Let the extensions of line segments \(\displaystyle AO\), \(\displaystyle BO\), \(\displaystyle CO\) intersect circle \(\displaystyle k\) at points \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\), respectively. Find the exact value of the area of the hexagon \(\displaystyle AC'BA'CB'\).

(5 pont)

Deadline expired on June 11, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit.

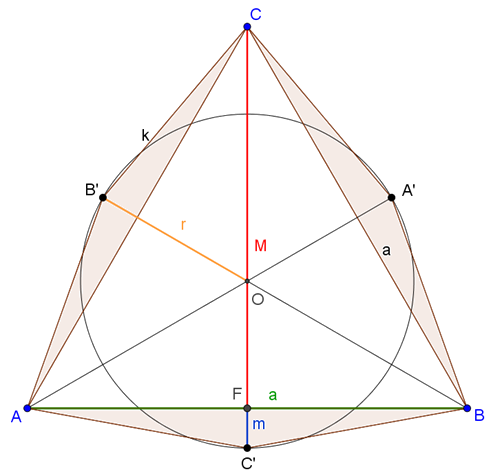
\(\displaystyle T_{kör}=T_Δ=\sqrt{\frac{π}{\sqrt{27}}}=r^2 π=\frac{a^2 \sqrt3}{4},\)

amiből

\(\displaystyle r=a\sqrt{\frac{\sqrt3}{4π}}.\)

Felhasználva, hogy \(\displaystyle M=a \frac{\sqrt3}{2}\), a felsőből

\(\displaystyle a^2=\frac{4}{\sqrt3}\cdot\sqrt{\frac{π}{\sqrt{27}}}= \sqrt{\frac{16π}{9\sqrt3}}.\)

\(\displaystyle m=r-\frac M3=a\cdot\left(\sqrt{\frac{\sqrt{3}}{4π}}-\frac{\sqrt3}{6}\right),\)

\(\displaystyle T_{ABC'}=\frac{am}{2}=\frac{a^2}{2} \left(\sqrt{\frac{\sqrt{3}}{4π}}-\frac{\sqrt3}{6}\right)=\)

\(\displaystyle =\sqrt{\frac{4π}{9\sqrt3}}\left(\sqrt{\frac{\sqrt{3}}{4π}}-\frac{\sqrt3}{6}\right)=\)

\(\displaystyle =\frac13-\frac13\frac{\sqrt{3}}{2}\sqrt{\frac{4π}{9\sqrt3}},\)

\(\displaystyle T_{ABC'}=\frac13-\frac13\sqrt{\frac{4π\cdot3}{4\cdot9\sqrt3}}=\frac13-\frac13\cdot\sqrt{\frac{π}{\sqrt{27}}},\)

\(\displaystyle T_{AB'CA'BC'}=T_Δ+3\cdot T_{ABC'}=\)

\(\displaystyle \sqrt{\frac{π}{\sqrt{27}}}+3\left(\frac13-\frac13\cdot\sqrt{\frac{π}{\sqrt{27}}}\right)=1.\)

Statistics:

75 students sent a solution.
5 points:	Agócs Katinka, Ajtai Boglárka, Almási Adél Csilla, Bérczi Péter, Biró 424 Ádám, Böcskei Bálint Attila, Bukor Benedek, Csóti Balázs , Csóti Kristóf, Debreczeni Tibor, Dékány Barnabás, Demcsák Ágnes, Fodor Marcel, Fonyi Máté Sándor, Forgács Kata, Gárdonyi Csilla Dóra, Gém Viktória, Hordós Adél Zita, Jankovits András, Kalabay László, Kis 194 Károly, Koleszár Domonkos, Kovács 157 Zita, Kovács 161 Márton Soma, Markó Gábor, Molnár 410 István, Németh Csilla Márta, Pinke Andrea, Rusvai Miklós, Shuborno Das, Surján Anett, Szécsi Adél Lilla, Székelyhidi Klára, Szőnyi Laura, Tóth 529 Petra, Tóth Imre, Trombitás Karolina Sarolta, Vlaszov Artúr, Williams Hajna.
4 points:	Andó Viola, Debreczeni Dorina, Földvári Ádám, Nagy 202 Eszter , Nyitrai Boglárka, Pszota Máté, Rittgasszer Ákos, Spányik Teodor, Szajkó Szilvia, Szőke Péter, Varga 928 Péter.
3 points:	12 students.
2 points:	2 students.
1 point:	4 students.
0 point:	3 students.
Unfair, not evaluated:	4 solutionss.

Problems in Mathematics of KöMaL, May 2018