Problem C. 1489. (May 2018)

C. 1489. In the lower left corner of a chessboard there is a black bishop, and in the lower right corner there is a white bishop. Each bishop moves up the board in steps of one unit, remaining on fields of its own colour. In each step, it may move to the left or to the right, at random, until it reaches the top row. What is the probability that the black bishop ends up to the right of the white bishop?

(5 pont)

Deadline expired on June 11, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Írjuk be a sakktábla mezőire, hogy a sötét futó az egyes mezőkre mekkora valószínűséggel juthat el.

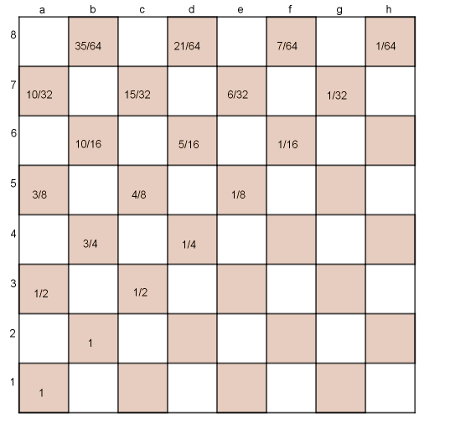
Kiinduláskor az a1 mezőn áll 1 valószínűséggel. Innen csak egy helyre mehet tovább, tehát a b2 valószínűsége is 1. Innen egyenlő valószínűséggel megy az a3, illetve a c3 mezőkre, így ezek valószínűsége 1/2–1/2. Az a3 mezőről 1 valószínűséggel a b4 mezőre lép, míg c3 mezőről 1/2–1/2 valószínűséggel lép tovább a b4, illetve a d4 mezőre. Tehát a b4 valószínűsége \(\displaystyle p(b4)=1\cdot1/2+1/2\cdot1/2=3/4\), míg d4 valószínűsége \(\displaystyle p(d4)=1/2\cdot1/4=1/8\).

A többi mezőt sorban hasonlóan kitöltve: \(\displaystyle p(a5)=1/2\cdot p(b4)=3/8\), \(\displaystyle p(c5)=1/2\cdot p(b4)+1/2\cdot p(d4)=4/8\),\(\displaystyle p(e5)=1/2\cdot p(d4)=1/8\), \(\displaystyle p(b6)=1\cdot3/8+1/2\cdot4/8=10/16\), \(\displaystyle p(d6)=1/2\cdot4/8+1/2\cdot1/8=5/16\), \(\displaystyle p(f6)=1/2\cdot1/8=1/16\), \(\displaystyle p(a7)=1/2\cdot10/16=10/32\), \(\displaystyle p(c7)=1/2\cdot10/16+1/2\cdot5/16=15/32\), \(\displaystyle p(e7)=1/2\cdot5/16+1/2\cdot1/16=6/32\), \(\displaystyle p(g7)=1/2\cdot1/16=1/32\), végül \(\displaystyle p(b8)=1\cdot10/32+1/2\cdot15/32=35/64\), \(\displaystyle p(d8)=1/2\cdot15/32+1/2\cdot6/32=21/64\), \(\displaystyle p(f8)=1/2\cdot6/32+1/2\cdot1/32=7/64\) és \(\displaystyle p(h8)=1/2\cdot1/32=1/64\).

Mivel a világos futó ugyanezen lépéseket fordítva teszi meg, így az ő esetében \(\displaystyle p(a8)=1/64\), \(\displaystyle p(c8)=7/64\), \(\displaystyle p(e8)=21/64\) és \(\displaystyle p(h8)=35/64\).

Tehát a valószínűségek balról jobbra: világos(1/64), sötét(35/64), világos(7/64), sötét(21/64), világos(21/64), sötét(7/64), világos(35/64), sötét(1/64).

Tehát annak valószínűsége, hogy a sötét futó a világos futótól jobbra érkezik a felső sorba:

\(\displaystyle p=\frac{35}{64}\cdot\frac{1}{64}+\frac{21}{64}\cdot\left(\frac{1+7}{64}\right)+\frac{7}{64}\cdot\left(\frac{1+7+21}{64}\right)+\frac{1}{64}\cdot\left(\frac{1+7+21+35}{64}\right)=\)

\(\displaystyle =\frac{470}{64^2}\approx0,115.\)

Statistics:

27 students sent a solution.
5 points:	Ajtai Boglárka, Molnár 410 István, Spányik Teodor.
3 points:	19 students.
2 points:	4 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, May 2018