Problem C. 1499. (October 2018)

C. 1499. Find the largest positive integer \(\displaystyle n\) for which there exists an appropriate order of the numbers \(\displaystyle 1,2,\ldots,n\) such that the large number obtained by writing all the numbers together in a row has the following property: for any pair \(\displaystyle a\), \(\displaystyle b\) of successive digits, at least one of the two-digit numbers \(\displaystyle \overline{ab}\), \(\displaystyle \overline{ba}\) is a prime.

(5 pont)

Deadline expired on November 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. \(\displaystyle n\geq10\) esetén a \(\displaystyle 0\) számjegy semelyik \(\displaystyle k\) számjeggyel sem teljesítheti a feltételt, mert \(\displaystyle \overline{k0}\) páros, \(\displaystyle \overline{0k}\) pedig nem kétjegyű. Tehát \(\displaystyle n\) legfeljebb \(\displaystyle 9\).

A feltétel miatt két páros számjegy egymás után nem állhat a számban. Tehát felváltva következnek páros és páratlan számjegyek, illetve egy helyen lehet egymás mellett két páratlan számjegy (ha \(\displaystyle n\) páratlan). Ha \(\displaystyle n\) páros, akkor csak olyan kétjegyű prímszámok jöhetnek szóba, melyek egyik (nyilván az első) számjegye páros. Ha \(\displaystyle n\) páratlan, akkor egy páratlan számjegyekből álló prímszám is lehet.

A kétjegyű prímszámok, melyek egyik számjegye páros: \(\displaystyle 23\), \(\displaystyle 29\), \(\displaystyle 41\), \(\displaystyle 43\), \(\displaystyle 47\), \(\displaystyle 61\), \(\displaystyle 67\), \(\displaystyle 83\), \(\displaystyle 89\).

Az \(\displaystyle 5\)-ös számjegy nem szerepel ezekben a számokban, és nem lehet egy kétjegyű prím második számjegye, így csak az első vagy utolsó számjegy lehet az összes szám között is. A szimmetria miatt azonban feltehetjük, hogy az első számjegy lesz. Az \(\displaystyle 5\)-ös számjegyet tartalmazó kétjegyű prímszámok az \(\displaystyle 53\) és az \(\displaystyle 59\). Ha \(\displaystyle 53\)-mal kezdjük a számot, akkor háromféleképpen folytathatjuk. Mindig a következő sorba írjuk a lehetséges folytatást. Látható, hogy nem tudunk minden számjegyet felhasználni, mert ismétlődnének a számjegyek. Ugyanezt kapjuk akkor, ha végignézzük az eseteket az \(\displaystyle 59\)-cel elkezdve.

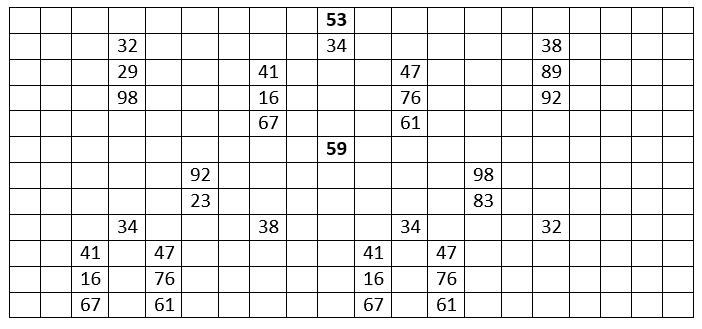
Tehát az \(\displaystyle 5\) nem szerepelhet a számjegyek között. Ha \(\displaystyle n=4\), akkor egy lehetséges sorrend: \(\displaystyle 2314\). Tehát \(\displaystyle n\) legfeljebb \(\displaystyle 4\) lehet.

Statistics:

242 students sent a solution.
5 points:	112 students.
4 points:	10 students.
3 points:	24 students.
2 points:	17 students.
1 point:	39 students.
0 point:	32 students.
Not shown because of missing birth date or parental permission:	8 solutions.

Problems in Mathematics of KöMaL, October 2018