Problem C. 1502. (October 2018)

C. 1502. In each figure, there are six circles of equal radius drawn in a unit square. In which arrangement do the circles have a larger radius?

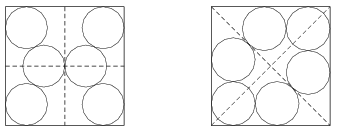
German competition problem

(5 pont)

Deadline expired on November 12, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Vizsgáljuk meg az első ábrát.

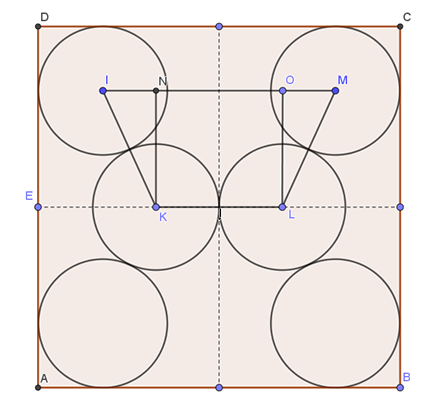
Az \(\displaystyle I\), \(\displaystyle K\), \(\displaystyle L\) és \(\displaystyle M\) pontokat összekötve a szimmetria miatt egyenlő szárú trapézt kapunk. Az \(\displaystyle E\) pont az egységnyi hosszú \(\displaystyle AD\) oldal felezőpontja, így az \(\displaystyle ED\) szakasz hossza fél egység. Legyen \(\displaystyle N\) és \(\displaystyle O\) a \(\displaystyle K\) és \(\displaystyle L\) pontokból az \(\displaystyle IM\) szakaszra állított merőlegesek (amik a trapéz magasságai) talppontja. Így az \(\displaystyle INK\) háromszög derékszögű. az \(\displaystyle IK\) szakasz hossza a kör sugarának (\(\displaystyle r\)) a kétszerese, mert az \(\displaystyle I\) és \(\displaystyle K\) középpontú körök érintik egymást, és a középpontokat összekötő szakasz átmegy az érintési ponton is. Az \(\displaystyle NK\) szakasz hosszát úgy kapjuk meg, ha az \(\displaystyle ED\) szakasz hosszából kivonjuk az \(\displaystyle IP\) szakasz hosszát, azaz a kör sugarát. Így \(\displaystyle NK=\frac12-r\).

Az \(\displaystyle IM\) szakasz hossza \(\displaystyle 1-2r\). \(\displaystyle KL=NO=2r\) és \(\displaystyle IN=OM\). Így \(\displaystyle IN=\frac{1-2r-2r}{2}\).

Alkalmazzuk Pitagorasz tételét az \(\displaystyle INK\) derékszögű háromszögön:

\(\displaystyle IN^2+NK^2=IK^2,\)

\(\displaystyle \left(\frac{1-4r}{2}\right)^2+\left(\frac12-r\right)^2=(2r)^2,\)

\(\displaystyle \frac{1-8r+16r^2}{4}+\frac14-r+r^2=4r^2,\)

\(\displaystyle 1-8r+16r^2+1-4r+4r^2=16r^2,\)

\(\displaystyle 4r^2-12r+2=0,\)

\(\displaystyle 2r^2-6r+1=0,\)

\(\displaystyle r_{1;2}=\frac{6±\sqrt{36-8}}{4}=\frac{6±\sqrt{28}}{4}=\frac{6±2\sqrt7}{4}=\frac{3±\sqrt7}{2}.\)

Ebből \(\displaystyle r_1≈2,82\), de ez nagyobb, mint az egységnyi oldal, ezért ez nem megoldás; illetve \(\displaystyle r_2=\frac{3-\sqrt7}{2}\), ez a körök sugara.

Most vizsgáljuk meg a 2. ábrát.

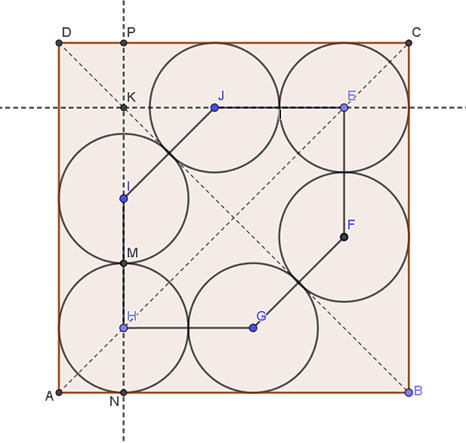
Az \(\displaystyle EJ\) és \(\displaystyle HI\) szakaszok meghosszabbításai a \(\displaystyle K\) pontban metszik egymást. Mivel \(\displaystyle HI||AD\) és \(\displaystyle EJ||BA\), ezért az \(\displaystyle IKJ\) háromszög derékszögű, továbbá a szimmetria miatt \(\displaystyle IK=JK\). \(\displaystyle IJ=2r\) és \(\displaystyle IK=1-4r\).

Írjuk fel Pitagorasz tételét az \(\displaystyle IKJ\) derékszögű háromszögre:

\(\displaystyle 2\cdot(1-4r)^2=(2r)^2,\)

\(\displaystyle 2\cdot(1-8r+16r^2)=4r^2,\)

\(\displaystyle 1-8r+16r^2=2r^2,\)

\(\displaystyle 14r^2-8r+1=0,\)

\(\displaystyle r_{1;2}=\frac{8±\sqrt{64-56}}{28}=\frac{8±\sqrt8}{28}=\frac{8±2\sqrt2}{28}=\frac{4±\sqrt2}{14}.\)

Ebből \(\displaystyle r_1≈0,4\), de ez túlságosan nagy az egységnyi oldalhoz képest, így nem megoldás; míg \(\displaystyle r_2=\frac{4-\sqrt2}{14}\), így ebben az esetben ennyi a körök sugara.

Mivel \(\displaystyle \frac{3-\sqrt7}{2}=0,177...\) és \(\displaystyle \frac{4-\sqrt2}{14}=0,184...\), így a második elrendezésben nagyobb a körök sugara.

Hordós Adél Zita (Kecskeméti Református Gimnázium, 11. évf.)

Statistics:

76 students sent a solution.
5 points:	Babolcsay Barbara, Gálffy Veronika, Hordós Adél Zita, Jankovits András, Kis 194 Károly, Kis-Tóth Janka, Kovács 111 Bence, Lénárd Kristóf, Mészáros 916 Márton, Molnár 410 István, Nyerges Péter, Nyitrai Boglárka, Rozgonyi Gergely, Rusvai Miklós, Sebe Anna, Szabó 314 László, Teleki Sándor, Varga Ákos, Veibli-Magyari Kristóf.
4 points:	Ajtai Boglárka, Ámmer Fanni, Paksi Barnabás, Ráduly Nóra Julianna, Sal Dávid, Schäffer Tamás, Szántai Gábor, Szőke Levente, Tóth Imre.
3 points:	7 students.
2 points:	9 students.
1 point:	3 students.
0 point:	16 students.
Unfair, not evaluated:	9 solutionss.
Not shown because of missing birth date or parental permission:	4 solutions.

Problems in Mathematics of KöMaL, October 2018