 Problem C. 1505. (November 2018)
Problem C. 1505. (November 2018)
C. 1505. Consider the circumscribed circles of all the black fields of a chessboard. What fraction of the total area of the 64 fields is covered by these disks altogether?
(5 pont)
Deadline expired on December 10, 2018.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először tekintsük két csúcsszomszédos sötét mező körülírt körét. Definíció szerint mindkét kör átmegy a négyzetek közös csúcsán. Szimmetriai okok miatt, ha ezen két körülírt körnek a csúcsokon kívül máshol is lenne közös pontja, akkor még kettő lenne, ami nem lehetséges, hiszen 2 különböző körnek 0, 1 vagy 2 metszéspontja lehet. Így a sötét mezők körülírt körei a csúcsokban érintik egymást, és a sötét mezőkön kívüli körszeleteik diszjunktak. Azaz így néz ki a sakktáblánk a sötét mezők körülírt köreivel:
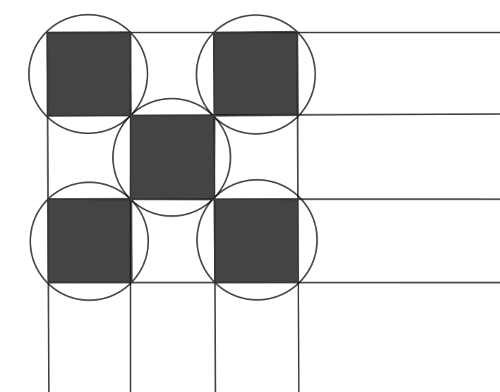
Vegyük észre, hogy háromféle sötét mezőt tudunk megkülönböztetni az alapján, hogy az adott mező körülírt körének hány ,,kilógó'' (az adott sötét mezőn kívül elehelyezkedő) körszelete esik a sakktáblán belülre:
1. eset: csak kettő: ezek a sarkokban levő sötét mezők, 2 db ilyen van,
2. eset: három: ezek a széleken, de nem sarokban levő sötét mezők: 12 db ilyen van,
3. eset: mind a négy: ezek a középső (sötét) mezők, \(\displaystyle 32-2-12=18\) db ilyen van.
Most számoljuk ki, hogy melyik esetben mekkora területet fed le egy-egy sötét mező körülírt köre a sakktáblából, ehhez vegyük a sakktábla mezőinek oldalhosszát 1 egységnek.
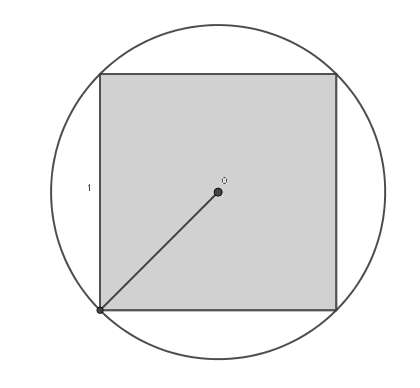
Ekkor a körülírt körének sugara (a Pitagorasz-tétel alapján) \(\displaystyle \frac{1}{\sqrt 2}\). A négyzet területe \(\displaystyle t_{\text{négyzet}}=1\), körülírt körének területe pedig \(\displaystyle t_{\text{kör}}=\frac{\pi}{2}\). Szimmetria okokból egy ,,kilógó'' körszelet területe: \(\displaystyle t_{\text{körszelet}}=\left(\frac{\pi}{2}-1\right) /4= \frac{\pi}{8}-\frac{1}{4}\).
Ezek alapján a sötét mezők kürülírt körei által lefedett terület:
\(\displaystyle t=2 \left[1+2\left(\frac{\pi}{8}-\frac{1}{4}\right)\right] + 12 \left[1+3\left(\frac{\pi}{8}-\frac{1}{4}\right)\right]+ 18\cdot \frac{\pi}{2} = \left(1+\frac{\pi}{2}\right)+\left(3+\frac{9\pi}{2}\right)+9 \pi,\)
\(\displaystyle t=4+14\pi.\)
A sakktábla területe \(\displaystyle t_{\text{sakktabla}}=64\), így a keresett arány:
\(\displaystyle \frac{t}{t_{\text{sakktabla}}}= \frac{4+ 14\pi}{64} \approx 0,7497.\)
Azaz a sakktábla sötét mezőinek körülírt körei a játéktér \(\displaystyle \frac{2+ 7\pi}{32}\)-ed részét fedik le.
Statistics:
246 students sent a solution. 5 points: 135 students. 4 points: 50 students. 3 points: 21 students. 2 points: 23 students. 1 point: 9 students. 0 point: 1 student. Not shown because of missing birth date or parental permission: 7 solutions.
Problems in Mathematics of KöMaL, November 2018
