Problem C. 1507. (November 2018)

C. 1507. The perpendicular bisectors of the legs of an obtuse-angled isosceles triangle divide the base into three equal parts. Find the measures of the angles.

(5 pont)

Deadline expired on December 10, 2018.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a háromszög \(\displaystyle ABC\), és legyen \(\displaystyle C\)-nél a tompaszög (és így \(\displaystyle AC=BC\)). Mivel tompaszögű háromszögről van szó, így az oldalfelezőmerőlegesek a háromszögön kívül metszik egymást, és ezért az \(\displaystyle AC\) oldal oldalfelezőmerőlegese az \(\displaystyle A\)-hoz közelebbi harmadolópontban metszi az \(\displaystyle AB\) alapot, a \(\displaystyle BC\) felezőmerőlegese pedig a \(\displaystyle B\)-hez közelebbi harmadolópontban. Legyenek az alapon lévő harmadolópontok \(\displaystyle G\) és \(\displaystyle H\) az ábra szerint, és ezeket kössük össze az alappal szemközti \(\displaystyle C\) csúccsal.

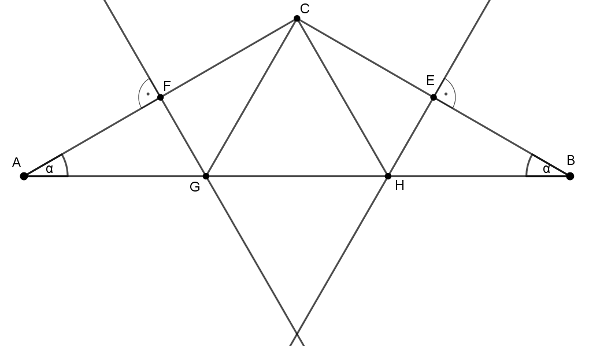
A feladat szövege alapján \(\displaystyle AG=GH=HB\). Vegyük észre, hogy mivel \(\displaystyle G\) rajta van \(\displaystyle AC\) felezőmerőlegesén, így \(\displaystyle AG=GC\). Azaz az \(\displaystyle AGC\) háromszög egyenlőszárú, \(\displaystyle CAG\angle =ACG\angle= \alpha.\) Ugyanígy \(\displaystyle BH=HC\), azaz a \(\displaystyle BHC\) háromszög is egyenlőszárú, és \(\displaystyle HBC\angle=BCH\angle=\alpha\). Továbbá a szakaszok egyenlőségét összevetve, kapjuk, hogy \(\displaystyle AG=GC=GH=HC=HB\). Tehát a \(\displaystyle GHC\) háromszög szabályos, mert mindhárom oldala egyenlő, és így minden szöge \(\displaystyle {60^\circ}\)-os.

Azaz az \(\displaystyle ABC\) háromszög szögei \(\displaystyle \alpha, \alpha, 60^\circ+ 2 \alpha\). Ebből

\(\displaystyle \alpha+ \alpha+ 60^\circ+ 2 \alpha=180^\circ.\)

Ezt összevonva és átrendezve kapjuk, hogy

\(\displaystyle 4 \alpha= 120^\circ,\)

azaz

\(\displaystyle \alpha=30^\circ.\)

Így a háromszög szögei \(\displaystyle 30^\circ, 30^\circ\) és \(\displaystyle 120^\circ\).

Végül ellenőrizzük, hogy ebben a háromszögben valóban teljesül az előírt feltétel. A korábban használt indoklás ,,megfordításával'' kapjuk, hogy ha \(\displaystyle AC\) és \(\displaystyle BC\) felezőmerőlegesének \(\displaystyle AB\)-vel vett metszéspontját rendre \(\displaystyle G\), illetve \(\displaystyle H\) jelöli, akkor \(\displaystyle AG=CG\) és \(\displaystyle BH=CH\), továbbá (szögszámolás alapján) a \(\displaystyle CGH\) háromszög szabályos. Így \(\displaystyle AG=CG=GH=CH=BH\), tehát \(\displaystyle G\) és \(\displaystyle H\) valóban harmadolópontok.

Statistics:

314 students sent a solution.
5 points:	237 students.
4 points:	35 students.
3 points:	2 students.
2 points:	12 students.
1 point:	6 students.
0 point:	7 students.
Not shown because of missing birth date or parental permission:	15 solutions.

Problems in Mathematics of KöMaL, November 2018