 |
A C. 1511. feladat (2018. december) |
C. 1511. Az \(\displaystyle AD\) szakasz \(\displaystyle B\) és \(\displaystyle C\) belső pontjaira \(\displaystyle AB=CD\) teljesül. Bizonyítsuk be, hogy ha \(\displaystyle P\) a sík egy tetszőleges pontja, akkor \(\displaystyle PA+PD\ge PB+PC\).
(5 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
Megoldás. Először legyen a pontok sorrendje az ábrán látható módon: \(\displaystyle A, B, C\) és \(\displaystyle D\), és tegyük fel, hogy \(\displaystyle P\) nincs az \(\displaystyle AB\) egyenesén. Tükrözzük a \(\displaystyle P\) pontot és az \(\displaystyle AD\) szakaszt az \(\displaystyle AD\) szakasz \(\displaystyle F\) felezőpontjára, legyen \(\displaystyle P\) képe \(\displaystyle Q\). Ennél a középpontos tükrözésnél \(\displaystyle A\) pont képe \(\displaystyle D\) és \(\displaystyle B\) pont képe \(\displaystyle C\), vagyis \(\displaystyle AP\) képe \(\displaystyle DQ\) és \(\displaystyle PB\) képe \(\displaystyle QC\).
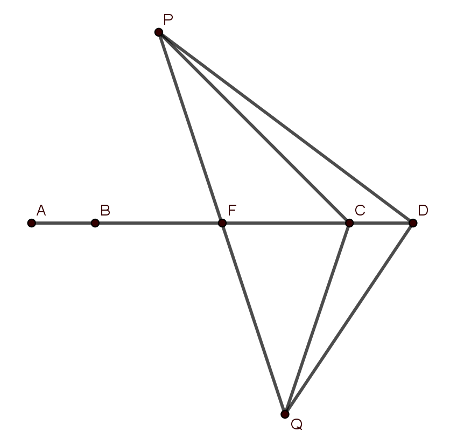
Ekkor a bizonyítandó állítás a középpontos tükrözés tulajdonságai miatt a következőképpen fogalmazható meg:
\(\displaystyle PD+QD \geq PC+QC.\)
Ez pedig teljesül, hiszen a \(\displaystyle PDQ\) háromszög tartalmazza a \(\displaystyle PCQ\) háromszöget, és ha egy háromszög egy másikat tartalmaz, akkor nagyobb a kerülete. (Ez a háromszög-egyenlőtlenség ismételt alkalmazásával könnyen igazolható, és háromszögek helyett tetszőleges konvex sokszögekre is teljesül – melyek közül az egyik tartalmazza a másikat.) Azaz a kívánt állítást ebben az esetben beláttuk.
Ha \(\displaystyle B\) és \(\displaystyle C\) közül \(\displaystyle C\) van közelebb \(\displaystyle A\)-hoz, akkor a fenti gondolatmenet ugyanígy működik (csak \(\displaystyle B\) és \(\displaystyle C\) szerepe felcserélődik). Ha \(\displaystyle B=C\), vagyis mindkét pont az \(\displaystyle AD\) oldal \(\displaystyle F\) felezőpontja, akkor is érvényesek a korábbiak, valójában ekkor az állítás egyetlen háromszög-egyenlőtlenség segítségével kapható: \(\displaystyle PB+PC=2PF=PQ<PD+QD=PA+PD\).
Végül, ha \(\displaystyle P\) rajta van az \(\displaystyle AD\) egyenesen, akkor az állítás nyilvánvalóan teljesül (amennyiben \(\displaystyle P\) az \(\displaystyle AD\) egyenes egy \(\displaystyle AD\) szakaszon kívül eső pontja vagy \(\displaystyle P\in\{A,D\}\), akkor egyenlőséggel).
Statisztika:
116 dolgozat érkezett. 5 pontot kapott: Ajtai Janka, Bana Marcell, Biró 424 Ádám, Bognár 171 András Károly, Buzás Bence István, Csilling Katalin, Csiszár Bence László, Csonka Illés, Debreczeni Dorina, Ecsedi Boglárka, Farkas Jázmin, Fonyi Máté Sándor, Hajdú Bálint, Halasi Tamás, Halász Henrik, Inokai Dávid, Kadem Aziz, Kara Zsombor, Kerekes Boldizsár, Kovács Gábor Benedek, Mácsai Dániel, Merkel Tamás, Mezey Dorottya, Mócza Levente András, Mócza Tamás István, Molnár Réka, Móricz 777 Anna, Nagy 551 Levente, Németh Imola, Németh Kristóf, Páhán Anita Dalma, Patricia Janecsko, Rékási Bence, Richlik Bence, Robin Eszter, Sas 202 Mór, Schenk Anna, Schneider Anna, Stein Felix, Szalanics Tamás, Trombitás Karolina Sarolta, Ungár Éva, Urszuly Csenge. 4 pontot kapott: 21 versenyző. 3 pontot kapott: 25 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 11 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2018. decemberi matematika feladatai

