Problem C. 1514. (December 2018)

C. 1514. A unit square is divided into four isosceles triangles by connecting an interior point to the vertices. Find the minimum and maximum values of the product of the areas of the four triangles.

(5 pont)

Deadline expired on January 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen \(\displaystyle A,B,C\) és \(\displaystyle D\) a négyzet 4 csúcsa, és \(\displaystyle e\), illetve \(\displaystyle f\) az \(\displaystyle AB\), illetve a \(\displaystyle BC\) oldal felezőmerőlegese. Nyilvánvaló, hogy \(\displaystyle e \cap f\) egy jó \(\displaystyle P\) pont. Ebben az esetben minden szárat \(\displaystyle P\) és egy csúcs közti szakasz alkot (melyek egyforma hosszúak).

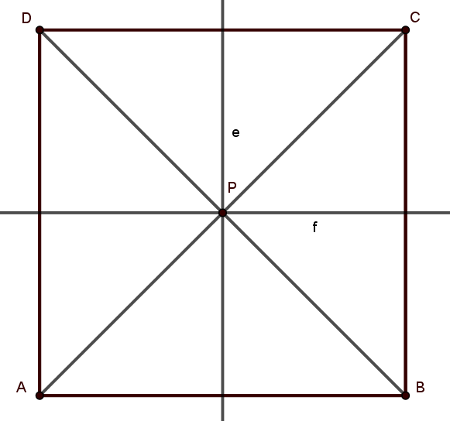
Ekkor mind a 4 egyenlőszárú háromszög területe \(\displaystyle \frac{1}{4}\), azaz a szorzatuk \(\displaystyle \left(\frac{1}{4}\right)^4=\frac{1}{256}.\)

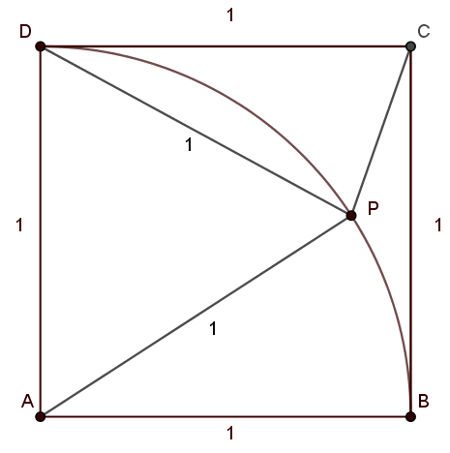
Most tegyük fel, hogy \(\displaystyle P \notin e,f\). Ilyenkor a háromszög egyik szára a négyzet oldala kell, hogy legyen. Nézzük először az \(\displaystyle APD\) háromszöget. Itt \(\displaystyle AD=1\), és például legyen \(\displaystyle AP=1.\) (A \(\displaystyle DP=1\) eset szimmetriai okokból ugyanígy megy.) Ekkor \(\displaystyle P\) rajta van az \(\displaystyle A\) középpontú egy sugarú (negyed)köríven. Most vegyük a \(\displaystyle DCP\) háromszöget. Ekkor két eset van:

1. eset: \(\displaystyle CD=CP=1\), ami nem lehetséges, hiszen ekkor \(\displaystyle P\)-nek rajta kellene lenni a \(\displaystyle C\) középpontú egy sugarú (negyed)köríven is. (A két (negyed)körív viszont \(\displaystyle B\)-ben és \(\displaystyle D\)-ben metszi egymást.)

2. eset \(\displaystyle CD=DP=1\). Ekkor viszont az \(\displaystyle ADP\) háromszög szabályos, azaz \(\displaystyle P\) rajta van \(\displaystyle f\)-en. Ez az ellentmondás mutatja, hogy \(\displaystyle P\) rajta van legalább az egyik oldalfelező merőlegesen.

Végül legyen \(\displaystyle P \in e,P\notin f\) (\(\displaystyle P \in f, P\notin e\) szimmetriai okokból ugyanígy megy). Ekkor az \(\displaystyle ADP\) háromszögben az egyik szár az \(\displaystyle AD\) (hiszen \(\displaystyle P\notin f\)), a másik pedig például az \(\displaystyle AP\), azaz \(\displaystyle AD=AP=1\). Mivel \(\displaystyle P \in e\), így az \(\displaystyle ABP\) háromszög egy 1 oldalú szabályos háromszög. Ekkor a \(\displaystyle BPC\) háromszögben \(\displaystyle BP\) és \(\displaystyle BC\) a két (1 hosszú) szár, tehát valóban mind a négy létrejövő háromszög egyenlő szárú. Ekkor az \(\displaystyle APD\) és a \(\displaystyle BPC\) háromszög területe \(\displaystyle \frac{1}{4}\), hiszen 1 az egyik oldal és \(\displaystyle \frac{1}{2}\) a hozzá tartozó magasság. A másik két háromszögből az egyik egy 1 oldalú szabályos háromszög, aminek a magassága \(\displaystyle \frac{\sqrt{3}}{2}\), a területe pedig \(\displaystyle \frac{\sqrt{3}}{4}\). Ekkor a negyedik háromszög területe \(\displaystyle \frac{1}{2}-\frac{\sqrt{3}}{4}=\frac{2-\sqrt{3}}{4}\). Ebben az esetben a háromszögek területének szorzata \(\displaystyle \frac{2\sqrt{3}-3}{256}\). Más eset pedig nincsen. (Tehát, ha \(\displaystyle P\) nem a négyzet középpontja, akkor csak a négyzet oldalára befelé állított szabályos háromszög harmadik csúcsa lehet.)

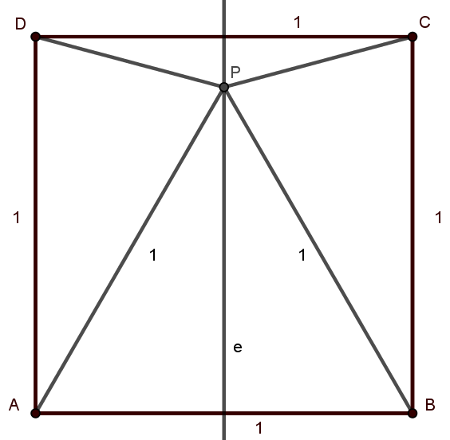
Azaz a keresett szorzat maximális értéke \(\displaystyle \frac{1}{256}\approx 0,0039\), minimális értéke pedig \(\displaystyle \frac{2\sqrt{3}-3}{256}\approx 0,0018\).

Statistics:

222 students sent a solution.
5 points:	131 students.
4 points:	33 students.
3 points:	19 students.
2 points:	23 students.
1 point:	5 students.
0 point:	2 students.
Not shown because of missing birth date or parental permission:	9 solutions.

Problems in Mathematics of KöMaL, December 2018