 |
A C. 1516. feladat (2018. december) |
C. 1516. Az \(\displaystyle O(4;-2)\) közepű, \(\displaystyle r=5\sqrt{3}\) sugarú körhöz érintőt húzunk a koordináta-rendszer \(\displaystyle P(16;7)\) pontjából. Az érintési pont merőleges vetületét az \(\displaystyle OP\) szakaszon jelölje \(\displaystyle P'\). Határozzuk meg \(\displaystyle P'\) koordinátáit.
(5 pont)
A beküldési határidő 2019. január 10-én LEJÁRT.
1. Megoldásvázlat. Végiggondoljuk, hogyan szerkesztenénk meg a \(\displaystyle P'\) pontot, és a szerkesztési lépéseket ültetjük át a koordinátageometria nyelvére. Azaz először meghatározzuk \(\displaystyle OP\) Thalesz-körének egyenletét: \(\displaystyle (x-10)^2+(y-2,5)^2=7,5^2\). Ennek és az eredeti körnek a metszéspontjai az érintési pontok.
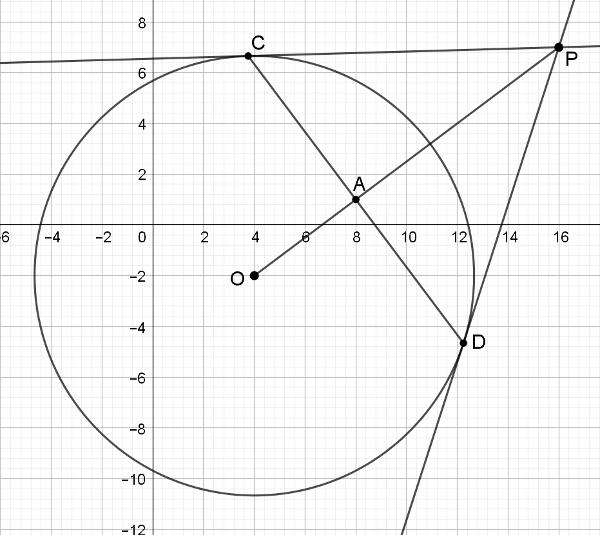
Az eredeti kör egyenlete: \(\displaystyle (x-4)^2+(y+2)^2=75\), a metszéspontok \(\displaystyle C(8-3\sqrt2,1+4\sqrt2)\) és \(\displaystyle D(8+3\sqrt2,1-4\sqrt2)\). Ennek a 2 pontnak ugyanaz a merőleges vetülete \(\displaystyle OP\)-re, hiszen bármely húr felezőmerőlegese átmegy a kör középpontján. Ez a merőleges vetület pedig nem más, mint az \(\displaystyle OP\) egyenes és a két érintési pont által meghatározott egyenes metszéspontja. Vagy egyszerűbben: a két metszéspont által meghatározott szakasz, \(\displaystyle CD\) felezőpontja, így koordinátái \(\displaystyle P'(8,1)\).
2. Megoldás.
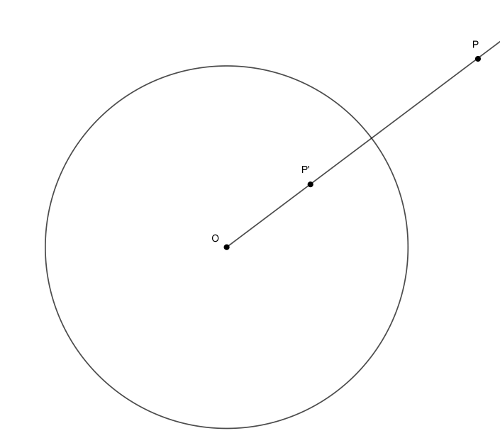
Vegyük észre, hogy a \(\displaystyle P'\) pont nem más, mint \(\displaystyle P\) képe az adott körre vonatkozó inverziónál, azaz
\(\displaystyle OP \cdot OP'=r^2.\)
Ide a megadott értékeket behelyettesítve kapjuk (\(\displaystyle OP\) meghatározásához a Pitagorasz-tételt használva), hogy
\(\displaystyle 15 \cdot OP'=75,\)
azaz
\(\displaystyle OP'=5.\)
Legyenek \(\displaystyle P'\) koordinátái \(\displaystyle (x',y')\). Ekkor
\(\displaystyle \sqrt{(x'-4)^2+(y'+2)^2}=5,\)
azaz
\(\displaystyle (x'-4)^2+(y'+2)^2=25. \)
Továbbá az inverzió definíciója szerint \(\displaystyle P'\) rajta van az \(\displaystyle OP\) félegyenesen, azaz koordinátái kielegítik az \(\displaystyle OP\) egyenes egyenletét. Most írjuk fel ennek az egyenesnek az egyenletét:
\(\displaystyle (y+2)(16-4)=(x-4)(7+2),\)
\(\displaystyle 3x-4y-20=0.\)
Ezután ide helyettesítsük be \(\displaystyle P'\) koordinátáit, és rendezzük át az egyenletet:
\(\displaystyle \frac{3x'-20}{4}=y'.\)
Ezt helyettesítsük vissza az \(\displaystyle OP'\)-re felírt egyenletbe:
\(\displaystyle (x'-4)^2+\left(\frac{3x'-12}{4}\right)^2=25,\)
\(\displaystyle \frac{25}{16}(x')^2-\frac{25}{2}x'+25=25,\)
\(\displaystyle \frac{25}{16}(x')^2-\frac{25}{2}x'=0.\)
Ebből
\(\displaystyle x'_{1,2}=0 \text{ és } 8.\)
Mivel \(\displaystyle P'\) rajta van az \(\displaystyle O\) kezdőpontú \(\displaystyle OP\) félegyenesen, így \(\displaystyle x' > 4\), azaz
\(\displaystyle x'=8.\)
Ezt visszahelyettesítve kapjuk, hogy
\(\displaystyle y'=1.\)
Tehát a \(\displaystyle P'\) pont koordinátái \(\displaystyle \left(8,1\right).\)
Megjegyzés. Gyorsabban is megkaphatjuk az eredményt: \(\displaystyle OP'=5\) alapján \(\displaystyle P'\) nem más mint az \(\displaystyle OP\) szakasz \(\displaystyle O\)-hoz közelebbi harmadolópontja, és így \(\displaystyle P'=(8,1)\).
Statisztika:
61 dolgozat érkezett. 5 pontot kapott: Ajtai Boglárka, Andorfi István, Bálint Dalma, Bárczi Enikő Anna, Bárdos Deák Botond, Debreczeni Tibor, Demcsák Ágnes, Facskó Vince, Falvay Júlia, Gálffy Veronika, Gárgyán Barnabás, Hordós Adél Zita, Horváth 142 Tamara, Jankovits András, Jelinek Dorka, Kalabay László, Kim 666 Levente, Király Róbert, Kis 194 Károly, Lénárd Kristóf, Limpek Balázs, Lukács Emma, Majerusz Ádám, Mészáros 916 Márton, Molnár 410 István, Nagy 202 Eszter , Nyitrai Boglárka, Pásti Bence, Rátki Luca, Richly Bálint, Rozgonyi Gergely, Rusvai Miklós, Sal Dávid, Schäffer Tamás, Sebe Anna, Szabó 677 Balázs István, Szabó Barbara Noémi, Székelyhidi Klára, Szigeti Donát, Tóth Imre, Varga Ákos, Wagner Dávid Barnabás. 4 pontot kapott: Mihalik Dániel, Német Franciska, Vándorffy Áron, Vlaszov Artúr. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 5 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 3 dolgozat.
A KöMaL 2018. decemberi matematika feladatai

