 |
A C. 1519. feladat (2019. január) |
C. 1519. Egy háromszög két oldalának hossza \(\displaystyle 31\) és \(\displaystyle 22\), a hozzájuk tartozó súlyvonalak merőlegesek egymásra. Mekkora a harmadik oldal?
(5 pont)
A beküldési határidő 2019. február 11-én LEJÁRT.
Megoldás.
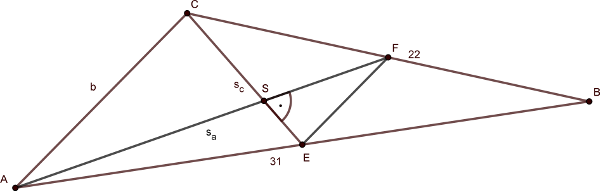
Legyen \(\displaystyle AB=31\) és \(\displaystyle CB=22\) a két megadott hosszúságú oldal. Legyen \(\displaystyle AB\) oldal felezőpontja \(\displaystyle E\), \(\displaystyle BC\)-é \(\displaystyle F\). Húzzuk be az \(\displaystyle EF\) középvonalat, majd írjuk fel a Pitagorasz-tételt a következő négy (\(\displaystyle S\)-nél) derékszögű háromszögre: \(\displaystyle AES\), \(\displaystyle FCS\), \(\displaystyle CAS\) és \(\displaystyle EFS\). Ezekből rendre kapjuk, hogy
\(\displaystyle \frac{4}{9}s_a^2+\frac{1}{9}s_c^2=240,25,\)
\(\displaystyle \frac{1}{9}s_a^2+\frac{4}{9}s_c^2=121,\)
\(\displaystyle \frac{4}{9}s_a^2+\frac{4}{9}s_c^2=b^2,\)
\(\displaystyle \frac{1}{9}s_a^2+\frac{1}{9}s_c^2=\frac{b^2}{4}.\)
(Felhasználtuk, hogy az \(\displaystyle S\) súlypont \(\displaystyle 2:1\) arányban osztja a súlyvonalakat.) Adjuk össze az első kettő, illetve a második kettő egyenletet, kapjuk
\(\displaystyle \frac{5}{9}s_a^2+\frac{5}{9}s_c^2=361,25,\)
\(\displaystyle \frac{5}{9}s_a^2+\frac{5}{9}s_c^2=\frac{5}{4}b^2.\)
Ebből
\(\displaystyle b^2=289,\)
azaz
\(\displaystyle b=17.\)
A háromszög harmadik oldala 17.
Megjegyzések. 1. A 31, 22 és 17 oldalhosszú háromszög két megfelelő súlyvonala tényleg merőleges egymásra, azaz létezik a feladatban szereplő háromszög.
2. A megoldás úgy is elmondható, hogy \(\displaystyle AEFC\) négyszög átlói pontosan akkor merőlegesek egymásra, ha az \(\displaystyle EC\) és \(\displaystyle AF\) átlók négyzetösszege megegyezik a négyszög oldalainak négyzetösszegével. (Ez az ismert állítás például éppen a megoldásban szereplő Pitagorasz-tételeken keresztül igazolható.)
Statisztika:
203 dolgozat érkezett. 5 pontot kapott: 152 versenyző. 4 pontot kapott: 18 versenyző. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 7 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 6 dolgozat.
A KöMaL 2019. januári matematika feladatai

