Problem C. 1519. (January 2019)

C. 1519. The lengths of two sides of a triangle are \(\displaystyle 31\) and \(\displaystyle 22\). The medians drawn to these sides are perpendicular. How long is the third side?

(5 pont)

Deadline expired on February 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

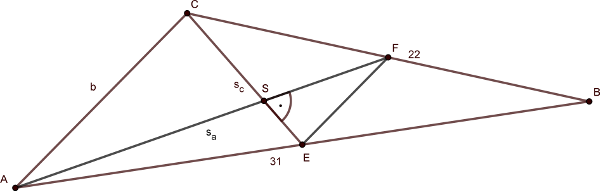
Legyen \(\displaystyle AB=31\) és \(\displaystyle CB=22\) a két megadott hosszúságú oldal. Legyen \(\displaystyle AB\) oldal felezőpontja \(\displaystyle E\), \(\displaystyle BC\)-é \(\displaystyle F\). Húzzuk be az \(\displaystyle EF\) középvonalat, majd írjuk fel a Pitagorasz-tételt a következő négy (\(\displaystyle S\)-nél) derékszögű háromszögre: \(\displaystyle AES\), \(\displaystyle FCS\), \(\displaystyle CAS\) és \(\displaystyle EFS\). Ezekből rendre kapjuk, hogy

\(\displaystyle \frac{4}{9}s_a^2+\frac{1}{9}s_c^2=240,25,\)

\(\displaystyle \frac{1}{9}s_a^2+\frac{4}{9}s_c^2=121,\)

\(\displaystyle \frac{4}{9}s_a^2+\frac{4}{9}s_c^2=b^2,\)

\(\displaystyle \frac{1}{9}s_a^2+\frac{1}{9}s_c^2=\frac{b^2}{4}.\)

(Felhasználtuk, hogy az \(\displaystyle S\) súlypont \(\displaystyle 2:1\) arányban osztja a súlyvonalakat.) Adjuk össze az első kettő, illetve a második kettő egyenletet, kapjuk

\(\displaystyle \frac{5}{9}s_a^2+\frac{5}{9}s_c^2=361,25,\)

\(\displaystyle \frac{5}{9}s_a^2+\frac{5}{9}s_c^2=\frac{5}{4}b^2.\)

Ebből

\(\displaystyle b^2=289,\)

azaz

\(\displaystyle b=17.\)

A háromszög harmadik oldala 17.

Megjegyzések. 1. A 31, 22 és 17 oldalhosszú háromszög két megfelelő súlyvonala tényleg merőleges egymásra, azaz létezik a feladatban szereplő háromszög.
2. A megoldás úgy is elmondható, hogy \(\displaystyle AEFC\) négyszög átlói pontosan akkor merőlegesek egymásra, ha az \(\displaystyle EC\) és \(\displaystyle AF\) átlók négyzetösszege megegyezik a négyszög oldalainak négyzetösszegével. (Ez az ismert állítás például éppen a megoldásban szereplő Pitagorasz-tételeken keresztül igazolható.)

Statistics:

203 students sent a solution.
5 points:	152 students.
4 points:	18 students.
3 points:	10 students.
2 points:	9 students.
1 point:	1 student.
0 point:	7 students.
Not shown because of missing birth date or parental permission:	6 solutions.

Problems in Mathematics of KöMaL, January 2019