 Problem C. 1526. (February 2019)
Problem C. 1526. (February 2019)
C. 1526. The circumscribed circle of a square is reflected in each side. Let \(\displaystyle T\) denote the area of the circle that touches these reflections in the interior of the square. Let \(\displaystyle t\) denote the area of the circle that touches one reflection and the circumscribed circle, both from the inside. Determine the smallest possible value of \(\displaystyle \frac{T}{t}\).
(5 pont)
Deadline expired on March 11, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen a négyzet oldala 2 (megjegyezzük, hogy az oldal bármennyinek választható, a feladat végeredményét nem befolyásolja, hiszen a területek arányát vizsgáljuk). Ekkor a körülírt körének sugara \(\displaystyle \sqrt{2}\). Először jegyezzük meg, hogy pontosan egy olyan kör létezik, ami a körülírt kör oldalakra vett tükörképeit a négyzet belsejében érinti, legyen ez \(\displaystyle K\), sugara pedig \(\displaystyle R\). Ekkor az ábra jelöléseit használva \(\displaystyle R= ON-2PN= \sqrt{2}-2(\sqrt{2}-1)=2-\sqrt{2}.\)
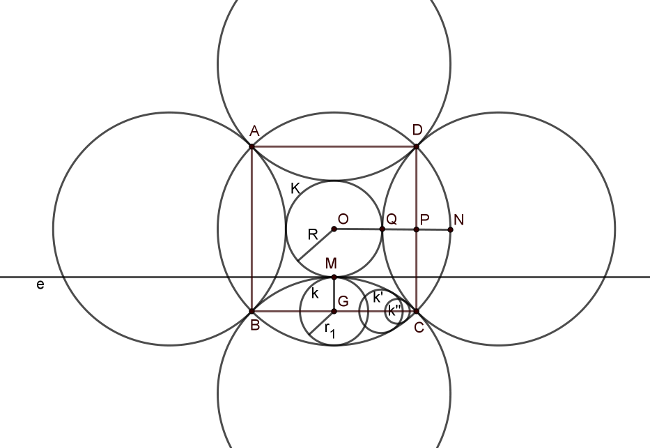
Másrészt olyan körből, ami egy tükörképet és a körülírt kört is belülről érinti végtelen sok van, például az ábrán \(\displaystyle k, k^{'} \text{ és } k^{''}\). Ezek területét jelölje rendre \(\displaystyle t, t^{'} \text{ és } t^{''}\). Ahhoz, hogy \(\displaystyle \frac{T}{t}\) lehetséges legkisebb értékét meghatározzuk, meg kell határozni \(\displaystyle t\) lehető legnagyobb értékét, hiszen \(\displaystyle T\) fix. Megmutatjuk, hogy a \(\displaystyle k\) kör területe a legnagyobb (természetesen szimmetria okokból 4 db ugyanekkora sugarú kör van, mindegyik tükörképhez tartozik egy). Ez pedig az a kör, ami a \(\displaystyle K\) kört ugyanabban az \(\displaystyle M\) pontban érinti, mint a tükörkép kör. Ehhez megmutatjuk, hogy a \(\displaystyle k\) kör sugara (\(\displaystyle r\)) a legnagyobb. Húzzuk be \(\displaystyle k\)-hoz \(\displaystyle M\)-ben az \(\displaystyle e\) érintőt. Ez párhuzamos a négyzet \(\displaystyle BC\) oldalával, valamint a tükörkép körnek is érintője. Mivel az érintőnek pontosan egy közös pontja van a körrel és az összes többi pontja külső pont, így \(\displaystyle e\)-nek nem lesz közös pontja a többi (\(\displaystyle k^{'}, k^{''}, \dots\)) körrel. Továbbá mivel az összes \(\displaystyle k\) kör középpontja \(\displaystyle BC\)-n, a közös húron van, így azok sugara biztosan kisebb \(\displaystyle r\)-nél.
Már csak az van hátra, hogy kiszámoljuk \(\displaystyle r\)-t: \(\displaystyle r=\sqrt{2}-1\). (A sugár értéke éppen \(\displaystyle PN\) hossza, ami \(\displaystyle ON\) és \(\displaystyle OP\) különbségeként megkapható, és értéke \(\displaystyle \sqrt{2}-1\).) Azaz \(\displaystyle \frac{T}{t}\) lehetséges legkisebb értéke
\(\displaystyle \frac{T}{t}=\frac{(2-\sqrt{2})^2 \pi}{(\sqrt{2}-1)^2 \pi}=2.\)
A keresett lehetséges legkisebb érték: \(\displaystyle 2\).
Statistics:
Problems in Mathematics of KöMaL, February 2019
