A C. 1529. feladat (2019. február)

C. 1529. Bizonyítsuk be, hogy bármely derékszögű háromszög felbontható \(\displaystyle 3k+2\) darab egyenlőszárú háromszögre tetszőleges \(\displaystyle k\) pozitív egész szám esetén.

(5 pont)

A beküldési határidő 2019. március 11-én LEJÁRT.

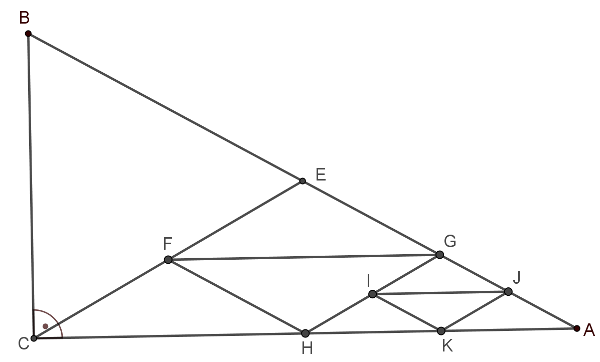
Megoldás. Használjuk az ábra jelöléseit. Először vegyük az \(\displaystyle AB\) átfogó felezőpontját (ami egyben a háromszög köréírt körének középpontja) ez legyen \(\displaystyle E\), majd kössük ezt össze \(\displaystyle C\)-vel. Ekkor az \(\displaystyle ABC\) háromszöget felbontottuk 2 egyenlőszárú háromszögre \(\displaystyle CAE\)-re és \(\displaystyle EBC\)-re (hiszen \(\displaystyle AE=BE=CE\)). Ezután elegendő már ezen egyenlőszárú háromszögek valamelyikét továbbontanunk egyenlőszárú háromszögekre. Válasszuk ki az egyik háromszögünket, például \(\displaystyle CAE\)-t, és húzzuk be a középvonalait. Ekkor 4 db (hozzá hasonló) egyenlőszárú háromszögre bontottuk fel \(\displaystyle CAE\)-t, így a háromszögeink száma 3-mal nőtt. Ezután a lépés után 5 egyenlőszárú háromszögre bontottuk a kiindulási derékszögű háromszögünket. Hasonló módon tetszőleges \(\displaystyle k\) mellett fel tudjuk bontani \(\displaystyle 3k+2\) egyenlőszárú háromszögre, hiszen először a fent említett módon 2-re osztjuk, majd \(\displaystyle k\)-szor ismételjük azt a lépést, hogy kiválasztjuk az egyik felbontásban szereplő egyenlőszárú háromszöget és a középvonalaival 4 kisebb egyenlőszárú háromszögre bontjuk. (Ahogy már említettük, minden ilyen lépésben 3-mal nő a háromszögek száma, így végül \(\displaystyle 3k+2\) lesz.)

Statisztika:

169 dolgozat érkezett.
5 pontot kapott:	129 versenyző.
4 pontot kapott:	33 versenyző.
3 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2019. februári matematika feladatai