 Problem C. 1544. (April 2019)
Problem C. 1544. (April 2019)
C. 1544. The diagonals of a circumscribed trapezium \(\displaystyle ABCD\) intersect at \(\displaystyle E\). The radii of the inscribed circles of triangles \(\displaystyle ABE\), \(\displaystyle BCE\), \(\displaystyle CDE\) and \(\displaystyle DAE\) are \(\displaystyle r_1\), \(\displaystyle r_2\), \(\displaystyle r_3\) and \(\displaystyle r_4\), respectively. Prove that
\(\displaystyle \frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}. \)
(5 pont)
Deadline expired on May 10, 2019.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A feladat szövege alapján az \(\displaystyle ABE\), \(\displaystyle BCE\), \(\displaystyle CDE\) és \(\displaystyle DAE\) háromszögekbe beírt körök sugarai rendre \(\displaystyle r_1\), \(\displaystyle r_2\), \(\displaystyle r_3\) és \(\displaystyle r_4\). Kerületük legyen rendre \(\displaystyle k_1\), \(\displaystyle k_2\), \(\displaystyle k_3\) és \(\displaystyle k_4\), területük pedig \(\displaystyle t_1\), \(\displaystyle t_2\), \(\displaystyle t_3\) és \(\displaystyle t_4\).
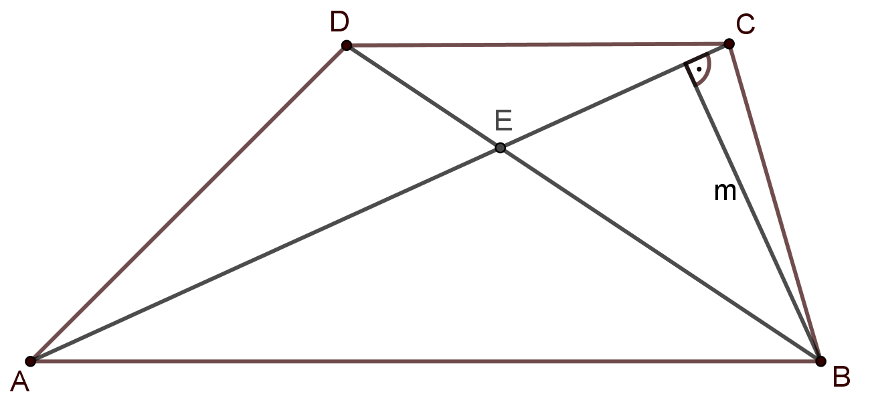
Mivel \(\displaystyle ABCD\) egy érintőnégyszög, így \(\displaystyle AB+CD=AD+BC\). Ebből következik, hogy
| \(\displaystyle k_1+k_3=k_2+k_4, \) | \(\displaystyle {(1)}\) |
hiszen mindkét oldal értéke \(\displaystyle AB+CD+AC+BD=AD+BC+AC+BD.\)
Másrészről \(\displaystyle ABCD\) egy trapéz, így
| \(\displaystyle t_2=t_4, \) | \(\displaystyle {(2)}\) |
hiszen mindkét oldalhoz \(\displaystyle ABE\) területét adva az \(\displaystyle ABC\), illetve \(\displaystyle ABD\) háromszögek területét kapjuk, ezen háromszögeknek pedig \(\displaystyle AB\) alapja, és ehhez tartozó magassága is közös.
Végül írjuk fel a \(\displaystyle t_1\) és \(\displaystyle t_2\) területek arányát a közös \(\displaystyle m\) magasságukat (lásd ábra) használva:
\(\displaystyle \frac{t_1}{t_2}=\frac{AE \cdot m}{EC \cdot m}=\frac{AE}{EC}.\)
Ugyanígy
\(\displaystyle \frac{t_4}{t_3}=\frac{AE}{EC}.\)
Amiből
\(\displaystyle \frac{t_1}{t_2}=\frac{t_4}{t_3},\)
azaz
| \(\displaystyle t_1 \cdot t_3= t_2 \cdot t_4. \) | \(\displaystyle {(3)}\) |
Meg kell mutatni, hogy
\(\displaystyle \frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}.\)
Az ismert területképlet (\(\displaystyle 2t_i=r_ik_i\)) szerint ezzel ekvivalens állítás a következő:
\(\displaystyle \frac{k_1}{t_1}+\frac{k_3}{t_3}=\frac{k_2}{t_2}+\frac{k_4}{t_4}.\)
A (2) és (3) összefüggésekből adódik, hogy \(\displaystyle t_2=t_4= \sqrt{t_1t_3}\). Ezt, illetve (1)-et használva kapjuk a következő ekvivalens alakot:
\(\displaystyle \frac{k_1}{t_1}+\frac{k_3}{t_3}=\frac{k_1+k_3}{\sqrt{t_1t_3}}.\)
Vegyük észre, hogy az \(\displaystyle ABE\) és \(\displaystyle ECD\) háromszögek hasonlóak (mindhárom szögük egyenlő), legyen a hasonlóság aránya \(\displaystyle 1:\alpha\). Ekkor \(\displaystyle k_3= \alpha k_1\) és \(\displaystyle t_3= \alpha^2 t_1\). Ezeket helyettesítsük be az egyenlőségünkbe:
\(\displaystyle \frac{k_1}{t_1}+\frac{\alpha k_1}{\alpha^2t_1}=\frac{k_1+\alpha k_1}{\sqrt{t_1 \alpha^2t_1}}.\)
Itt elvégezve az egyszerűsítéseket és \(\displaystyle t_1/k_1\)-gyel szorozva kapjuk az előzővel ekvivalens
\(\displaystyle 1+ \frac{1}{\alpha}=\frac{1+\alpha}{\alpha}\)
összefüggést. Ez igaz, így mivel végig ekvivalens átalakításokat hajtottunk végre, ezért az eredeti állítás is az.
Statistics:
22 students sent a solution. 5 points: Ajtai Boglárka, Hordós Adél Zita, Jankovits András, Kalabay László, Majerusz Ádám, Mészáros 916 Márton, Molnár 410 István, Nyitrai Boglárka, Rozgonyi Gergely, Sebe Anna, Székelyhidi Klára, Szigeti Donát. 4 points: Kis 194 Károly. 3 points: 1 student. 2 points: 1 student. 1 point: 3 students. 0 point: 4 students.
Problems in Mathematics of KöMaL, April 2019
