 |
A C. 1549. feladat (2019. május) |
C. 1549. Az \(\displaystyle AB\) szakasz felezőpontja legyen \(\displaystyle F\), továbbá legyen az \(\displaystyle AF\) szakasz egy tetszőleges pontja \(\displaystyle Z\). \(\displaystyle F\)-ben merőlegest állítunk \(\displaystyle AB\)-re és felmérjük rá az \(\displaystyle {FX=FA}\) távolságot. \(\displaystyle B\)-ben is merőlegest állítunk \(\displaystyle AB\)-re és felmérjük rá a \(\displaystyle BY=AZ\) távolságot úgy, hogy \(\displaystyle X\) és \(\displaystyle Y\) az \(\displaystyle AB\) egyenesének egyazon oldalán legyenek. Mekkora lehet az \(\displaystyle XZY\) szög?
Javasolta: Surányi László (Budapest)
(5 pont)
A beküldési határidő 2019. június 11-én LEJÁRT.
Megoldás. Készítsünk ábrát geogebrában, hátha megsejtünk valamit. Az alábbi letölthető fájl egy geogebra fájl, melyben a \(\displaystyle Z\) pont mozgatható az \(\displaystyle AF\) szakaszon. Ez alapján az a sejtés, hogy a kérdéses szög értéke \(\displaystyle 45^{\circ}\), sőt, az is a sejtés része lehet, hogy az \(\displaystyle XYZ\) háromszög egyenlő szárú és derékszögű.
Bizonyítsuk be.
Ha a \(\displaystyle Z\) pont az \(\displaystyle A\) pontba esik, akkor az \(\displaystyle Y\) pont a \(\displaystyle B\) ponttal egyezik meg, és az \(\displaystyle XZY\) háromszög egyenlő szárú derékszögű háromszög, \(\displaystyle XZY\angle=45^{\circ}\).

Ha a \(\displaystyle Z\) pont az \(\displaystyle F\) pontba esik, akkor az \(\displaystyle XZBY\) négyszög négyzet, az \(\displaystyle XZY\) háromszög egyenlő szárú derékszögű háromszög, \(\displaystyle XZY\angle=45^{\circ}\).
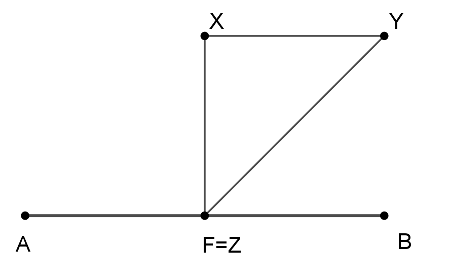
Ha a \(\displaystyle Z\) pont máshol helyezkedik el, arra az esetre adunk két megoldást.
1. megoldás.
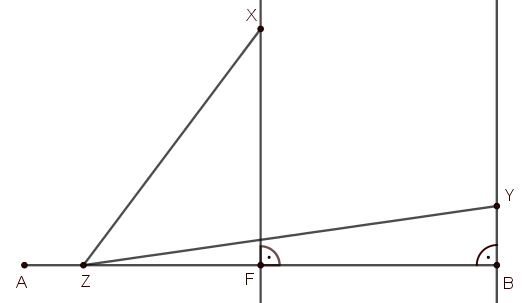
Feltehető, hogy \(\displaystyle AF=FB=FX=1\). Továbbá legyen \(\displaystyle AZ=z\neq1\), \(\displaystyle XZF \angle = \alpha\) és \(\displaystyle YZB \angle= \beta\). Ekkor a keresett szög \(\displaystyle XZY \angle = \alpha - \beta\). (Világos, hogy \(\displaystyle \beta\leq 45^\circ\leq \alpha\).)
Nézzük meg a szögek tangensét:
\(\displaystyle \tg \alpha = \frac{1}{1-z}\)
és
\(\displaystyle \tg \beta= \frac{z}{2-z}.\)
Most vizsgáljuk meg \(\displaystyle \alpha - \beta\) tangensét, használjuk az addiciós tételt, és írjuk be a fenti összefüggéseinket:
\(\displaystyle \tg (\alpha - \beta)= \frac{\tg \alpha - \tg \beta}{1+ \tg \alpha \tg \beta} = \frac{\frac{1}{1-z}-\frac{z}{2-z}}{1+\frac{z}{(1-z)(2-z)} }= \frac{(2-z)- z(1-z)}{(1-z)(2-z)+z}=\frac{z^2-2z+2}{z^2-2z+2}=1.\)
Azaz \(\displaystyle \tg XZY \angle=1\) és mivel \(\displaystyle XZY \angle\) hegyesszög, így \(\displaystyle XZY \angle= 45^\circ\).
Azaz a keresett \(\displaystyle XZY\) szög \(\displaystyle 45^\circ\).
Ha \(\displaystyle AZ=1\), akkor a \(\displaystyle Z\) pont megegyezik az \(\displaystyle F\) ponttal.
2. megoldás.
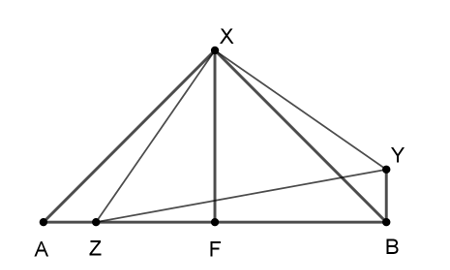
\(\displaystyle AFX\) és \(\displaystyle XFB\) egyenlő szárú derékszögű háromszögek, így \(\displaystyle AX=BX\) és \(\displaystyle XAF\angle=XBF\angle=45^{\circ}\). Ez utóbbiból \(\displaystyle XBY\angle=FBY\angle-XBF\angle=90^{\circ}-45^{\circ}=45^{\circ}\).
Mivel \(\displaystyle AZ=BY\), \(\displaystyle AX=BX\) és \(\displaystyle XAZ\angle=XBY\angle(=45^{\circ})\), ezért az \(\displaystyle AZX\) és a \(\displaystyle BYX\) háromszögek egybevágóak. Emiatt \(\displaystyle XZ=XY\) és \(\displaystyle AXZ\angle=BXY\angle\) is teljesül.
Mivel \(\displaystyle AXB\angle=45^{\circ}+45^{\circ}=90^{\circ}\), ezekből már következik, hogy \(\displaystyle ZXY\angle=ZXB\angle+BXY\angle=ZXB\angle+AXZ\angle=AXB\angle=90^{\circ}\). tehát az \(\displaystyle XYZ\) háromszög is egyenlő szárú és derékszögű, így \(\displaystyle XZY\angle=45^{\circ}\).
Statisztika:
91 dolgozat érkezett. 5 pontot kapott: 62 versenyző. 4 pontot kapott: 11 versenyző. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 11 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2019. májusi matematika feladatai

