 |
A C. 1554. feladat (2019. szeptember) |
C. 1554. Egy téglalapot, amelynek egyik oldala \(\displaystyle \frac{1+\sqrt5}{2}\)-szöröse a másiknak, átdaraboltunk egy vele egyenlő területű négyzetté. Hányszorosa a téglalap átlója a négyzetének?
(5 pont)
A beküldési határidő 2019. október 10-én LEJÁRT.
Megoldás. Legyen a feladatban szereplő téglalap rövidebb oldala \(\displaystyle a\), ekkor a hosszabb oldal \(\displaystyle \frac{1+\sqrt5}{2} a\). A téglalap területe pedig
\(\displaystyle T=\frac{1+\sqrt5}{2} a^2.\)
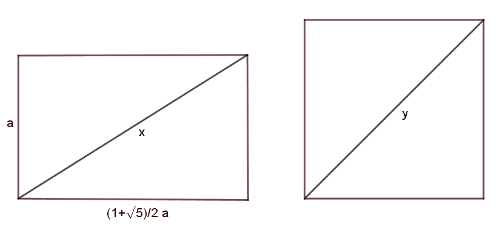
A vele egyenlő területű négyzet oldala emiatt \(\displaystyle \sqrt{\frac{1+\sqrt5}{2}} a\). Az ábrán látható módon a téglalap átlója legyen \(\displaystyle x\), a négyzeté \(\displaystyle y\).
Ekkor a Pitagorasz-tételt alkalmazva kapjuk, hogy:
\(\displaystyle x=\sqrt{a^2+\left(\frac{1+\sqrt5}{2} \right)^2 a^2},\)
\(\displaystyle y= \sqrt{\frac{1+\sqrt5}{2} a^2+ \frac{1+\sqrt5}{2} a^2}.\)
Az \(\displaystyle \frac{x}{y}\) arányt kell meghatározni, \(\displaystyle a\)-val rögtön egyszerűsítve kapjuk:
\(\displaystyle \frac{x}{y}= \sqrt{\frac{1+\left(\frac{1+\sqrt5}{2} \right)^2}{1+\sqrt{5}}} =\sqrt{\frac{\frac{4+(6+2\sqrt5)}{4}}{1+\sqrt5}}=\sqrt{\frac{\frac{5+\sqrt5}{2}}{1+\sqrt5}}=\)
\(\displaystyle =\sqrt{\frac{5+\sqrt5}{2+2\sqrt5}}= \sqrt{\frac{(5+\sqrt5)(2-2\sqrt5)}{(2+2\sqrt5)(2-2\sqrt5)}}=\sqrt{\frac{-8\sqrt5}{-16}} =\sqrt{\frac{\sqrt5}{2}}.\)
Azaz a téglalap átlója \(\displaystyle \sqrt{\frac{\sqrt5}{2}}=\sqrt[4]{\frac{5}{4}}\)-szerese, vagyis körülbelül \(\displaystyle 1,0574\)-szerese a négyzet átlójának.
Statisztika:
188 dolgozat érkezett. 5 pontot kapott: 116 versenyző. 4 pontot kapott: 30 versenyző. 3 pontot kapott: 16 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 9 versenyző. Nem versenyszerű: 7 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 2 dolgozat.
A KöMaL 2019. szeptemberi matematika feladatai

