Problem C. 1554. (September 2019)

C. 1554. One side of a rectangle is \(\displaystyle \frac{1+\sqrt5}{2}\) times as long as the other side. The rectangle is dissected and put together to form a square of the same area. What is the ratio of the diagonal of the rectangle to the diagonal of the square?

(5 pont)

Deadline expired on October 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a feladatban szereplő téglalap rövidebb oldala \(\displaystyle a\), ekkor a hosszabb oldal \(\displaystyle \frac{1+\sqrt5}{2} a\). A téglalap területe pedig

\(\displaystyle T=\frac{1+\sqrt5}{2} a^2.\)

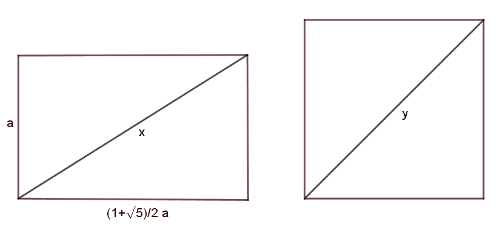
A vele egyenlő területű négyzet oldala emiatt \(\displaystyle \sqrt{\frac{1+\sqrt5}{2}} a\). Az ábrán látható módon a téglalap átlója legyen \(\displaystyle x\), a négyzeté \(\displaystyle y\).

Ekkor a Pitagorasz-tételt alkalmazva kapjuk, hogy:

\(\displaystyle x=\sqrt{a^2+\left(\frac{1+\sqrt5}{2} \right)^2 a^2},\)

\(\displaystyle y= \sqrt{\frac{1+\sqrt5}{2} a^2+ \frac{1+\sqrt5}{2} a^2}.\)

Az \(\displaystyle \frac{x}{y}\) arányt kell meghatározni, \(\displaystyle a\)-val rögtön egyszerűsítve kapjuk:

\(\displaystyle \frac{x}{y}= \sqrt{\frac{1+\left(\frac{1+\sqrt5}{2} \right)^2}{1+\sqrt{5}}} =\sqrt{\frac{\frac{4+(6+2\sqrt5)}{4}}{1+\sqrt5}}=\sqrt{\frac{\frac{5+\sqrt5}{2}}{1+\sqrt5}}=\)

\(\displaystyle =\sqrt{\frac{5+\sqrt5}{2+2\sqrt5}}= \sqrt{\frac{(5+\sqrt5)(2-2\sqrt5)}{(2+2\sqrt5)(2-2\sqrt5)}}=\sqrt{\frac{-8\sqrt5}{-16}} =\sqrt{\frac{\sqrt5}{2}}.\)

Azaz a téglalap átlója \(\displaystyle \sqrt{\frac{\sqrt5}{2}}=\sqrt[4]{\frac{5}{4}}\)-szerese, vagyis körülbelül \(\displaystyle 1,0574\)-szerese a négyzet átlójának.

Statistics:

188 students sent a solution.
5 points:	116 students.
4 points:	30 students.
3 points:	16 students.
2 points:	4 students.
1 point:	4 students.
0 point:	9 students.
Unfair, not evaluated:	7 solutionss.
Not shown because of missing birth date or parental permission:	2 solutions.

Problems in Mathematics of KöMaL, September 2019