Problem C. 1556. (September 2019)

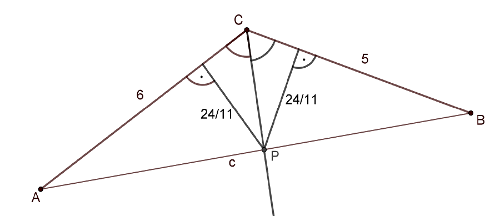
C. 1556. The interior angle bisector drawn from vertex \(\displaystyle C\) of triangle \(\displaystyle ABC\) intersects the opposite side at point \(\displaystyle P\). The distance of point \(\displaystyle P\) from the sides is \(\displaystyle \frac{24}{11}\), and \(\displaystyle AC=6\), \(\displaystyle BC=5\). Find the length of side \(\displaystyle AB\).

(5 pont)

Deadline expired on October 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle ABC\) háromszög területe felírható, mint az \(\displaystyle APC\) és a \(\displaystyle PBC\) háromszögek területének összege:

\(\displaystyle T_{ABC}= \frac{6 \cdot \frac{24}{11}}{2}+\frac{5 \cdot \frac{24}{11}}{2} =12.\)

Másrészről az \(\displaystyle ABC\) háromszög területét felírhatjuk a Hérón-képlet segítségével is:

\(\displaystyle T_{ABC}= \sqrt{\frac{11+c}{2} \cdot \frac{11+c-10}{2} \cdot \frac{11+c-12}{2} \cdot \frac{11+c-2c}{2}}= \sqrt{\frac{11+c}{2}\cdot\frac{1+c}{2}\cdot\frac{-1+c}{2}\cdot\frac{11-c}{2}}=\)

\(\displaystyle =\sqrt{\frac{(11^2-c^2)(c^2-1)}{2^4}}= \sqrt{\frac{-c^4+122c^2-121}{16}}.\)

Ezekből

\(\displaystyle 12=\sqrt{\frac{-c^4+122c^2-121}{16}},\)

ezt négyzetre emelve, átszorozva, majd egy oldalra rendezve:

\(\displaystyle 144=\frac{-c^4+122c^2-121}{16},\)

\(\displaystyle 2304=-c^4+122c^2-121,\)

\(\displaystyle c^4-122c^2+2425=0.\)

Ez egy \(\displaystyle c^2\)-ben másodfokú egyenlet. Alkalmazva a másodfokú egyenlet megoldóképletét kapjuk, hogy \(\displaystyle c^2\) értéke 25 vagy 97 lehet. Mivel \(\displaystyle c\) pozitív, ezért

\(\displaystyle c= 5 \text{ vagy } \sqrt{97}.\)

Az \(\displaystyle AB\) oldal hossza \(\displaystyle \sqrt{97} \text{ vagy } 5\).

Mindkét lehetőség valóban előfordulhat, hiszen az így kapott háromszögek léteznek (teljesülnek a háromszög-egyenlőtlenségek az oldalakra), és a Hérón-képlet szerint területük 12. A \(\displaystyle P\) pont az \(\displaystyle AC\) és \(\displaystyle BC\) oldalaktól egyforma távolságra kell legyen, hiszen a szögfelezőn van, így a fenti egyenlet alapján ennek a távolságnak \(\displaystyle \frac{24}{11}\)-nek kell lennie, hogy az \(\displaystyle APC\) és \(\displaystyle BPC\) háromszögek területének összege kiadja a 12-t.

Statistics:

239 students sent a solution.
5 points:	110 students.
4 points:	16 students.
3 points:	57 students.
2 points:	25 students.
1 point:	13 students.
0 point:	10 students.
Unfair, not evaluated:	8 solutionss.

Problems in Mathematics of KöMaL, September 2019