 |
A C. 1559. feladat (2019. szeptember) |
C. 1559. Egy tetraéder alaplapja szabályos háromszög, síkba kiterített palástja pedig olyan trapéz, melynek oldalai 10, 10, 10 és 14 egység hosszúak. Adjuk meg a tetraéder éleinek összhosszát és felszínét.
(5 pont)
A beküldési határidő 2019. október 10-én LEJÁRT.
Megoldás. Legyenek a tetraéder csúcsai \(\displaystyle A,B,C, D\) és élei \(\displaystyle a,b,c,d,d,d\) az ábrán látható módon.
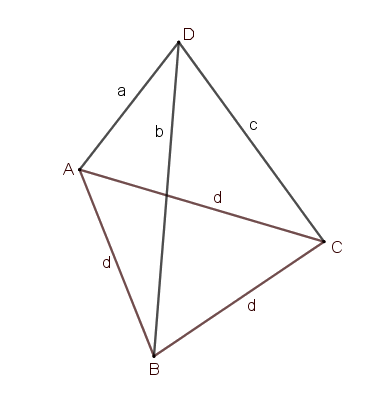
A tetraéder palástját terítsük ki a síkba úgy, hogy azt a \(\displaystyle BD\) él mentén vágjuk fel. (Megjegyezzük, hogy szimmetriai okokból feltehető, hogy a \(\displaystyle BD\) él mentén ,,vágtuk fel'' a palástot.)
A kiterített palást általános esetben a \(\displaystyle CAB''DB'\) ötszög lenne, azonban ez most a feltétel szerint egy trapéz. Ez csak úgy lehet, ha a \(\displaystyle B'DB''\) szög egyenesszög. (Ha az egyenesszög \(\displaystyle A\)-nál vagy \(\displaystyle C\)-nél lenne, akkor \(\displaystyle 2d\) is szerepelne az oldalak között, aminek 20-nak kellene lennie. \(\displaystyle B'\)-nél vagy \(\displaystyle B''\)-nél szintén nem lehet egyenesszög, hiszen az ott lévő szögek egy-egy háromszög belső szögei.)
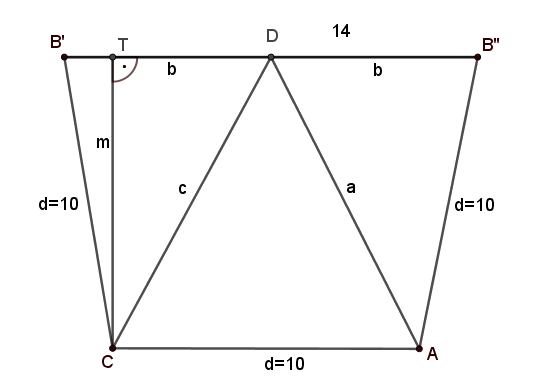
Mivel a palást ebben az esetben a feltétel szerint egy \(\displaystyle 10,10,10,14\) oldalhosszú trapéz, így \(\displaystyle 2b=14\), vagyis \(\displaystyle b=7.\) Mivel \(\displaystyle CB'=AB''\), ezért a trapéz vagy húrtrapéz, vagy paralelogramma. Mivel azonban \(\displaystyle AC\neq B'B''\), ezért ez utóbbi nem lehetséges. Tehát húrtrapézről van szó, és így a \(\displaystyle CB'D\) és \(\displaystyle AB''D\) háromszögek egybevágók (megegyezik két oldaluk és az általuk közbezárt szög), így \(\displaystyle a=c\).
Mivel a trapéz szimmetrikus, ezért a \(\displaystyle CTB'\) háromszögben a \(\displaystyle TB'\) oldal hossza \(\displaystyle (14-10)/2=2\) egység. Itt alkalmazva a Pitagorasz-tételt kapjuk, hogy a trapéz magassága
\(\displaystyle m=\sqrt{100-4}=\sqrt{96}.\)
Ezt felhasználva a \(\displaystyle TCD\) háromszögben (ahol a \(\displaystyle TD\) oldal hossza: \(\displaystyle 7-2=5\) egység) alkalmazva a Pitagorasz-tételt adódik, hogy
\(\displaystyle c=\sqrt{96+25}=11.\)
Innen a tetraéder éleinek összhossza
\(\displaystyle 10+10+10+7+11 + 11=59,\)
felszíne pedig a trapéz (palást) és az alapháromszög területének összege:
\(\displaystyle A= \frac{(10+14)\sqrt{96}}{2}+ \frac{10^2 \sqrt{3}}{4} = 48 \sqrt6 +25 \sqrt3.\)
Azaz a tetraéder éleinek összhossza \(\displaystyle 59\), felszíne pedig \(\displaystyle 48 \sqrt6 +25 \sqrt3(=\approx160,8768)\).
Statisztika:
85 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Antal Virág Anna, Arató Zita, Bakk Jázmin, Biró 424 Ádám, Blázsik Árpád, Bödő Lajos, Csizmadia Máté Zalán, Csizy Gergő , Fiam Regina, Gál Bence, Hajdú Bálint, Hodosi Rozi, Kinyó Kincső, Király Lénárd, Kis 194 Károly, Majerusz Ádám, Molnár Réka, Nagy 009 Dávid, Németh Kristóf, Oláh 492 Emese, Palencsár Enikő, Pásti Bence, Rátki Gergely, Schneider Anna, Szabó 808 Álmos Levente, Szabó Barbara Noémi, Szabó Csege, Székelyhidi Klára, Szigeti Donát, Szilágyi Dorka Szirka, Tompos Anna, Tuscher Dóra . 4 pontot kapott: Dinh Quocbao Róbert, Féger Tamás, Fekete András Albert, Gömbös Imola, Heller-Szabó Anna, Kadem Aziz, Koczó Attila, Kovács Bence, Lukács Emma, Ráduly Nóra Julianna, Rusvai Miklós, Slézia Dávid, Szarkowicz Dániel, Szeibel Richard, Wagner Dávid Barnabás, Zaránd Andris. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 12 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2019. szeptemberi matematika feladatai

