Problem C. 1561. (October 2019)

C. 1561. What may be the angles of a triangle, if the triangle formed by the points of tangency of the incircle on the sides is similar to the original triangle?

(5 pont)

Deadline expired on November 11, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit, a kiindulási háromszög \(\displaystyle ABC\), szögei \(\displaystyle \alpha,\beta,\gamma\).

A feladat szövege alapján az \(\displaystyle ABC\) és \(\displaystyle DEF\) háromszög hasonló, azaz a \(\displaystyle DEF\) háromszög szögei is \(\displaystyle \alpha, \beta, \gamma\) valamilyen sorrendben.

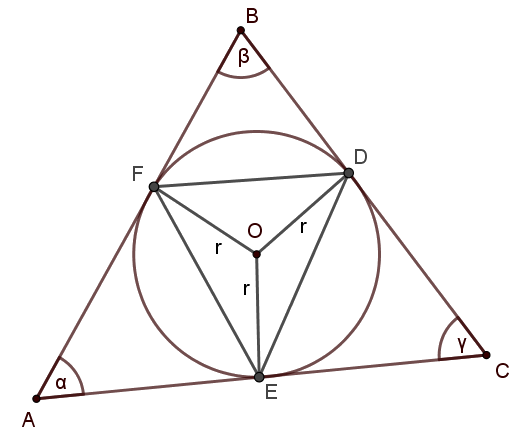
Először jegyezzük meg, hogy \(\displaystyle OFB \angle = ODB \angle= 90^\circ\), mert egy körhöz húzott külső érintő merőleges az érintési pontba húzott sugárra. Ekkor az \(\displaystyle ODBF\) négyszöget nézve kapjuk, hogy \(\displaystyle FOD \angle= 360^\circ - 2 \cdot 90^\circ- \beta = \alpha + \gamma.\) Mivel az \(\displaystyle OFD\) háromszög egyenlőszárú (két oldala sugár a beírt körben), így \(\displaystyle OFD \angle= ODF \angle = (180^\circ - (\alpha + \gamma))/2= \beta/2.\) Hasonlóan belátható, hogy az \(\displaystyle EFO\), illetve \(\displaystyle EDO\) egyenlőszárú háromszögek szárszögei rendre \(\displaystyle \alpha/2\), illetve \(\displaystyle \gamma/2\). Vagyis azt kaptuk, hogy az \(\displaystyle FED\) háromszög szögei \(\displaystyle \alpha/2+ \beta/2, \alpha/2+ \gamma/2, \beta/2+ \gamma/2\).

A feltétel szerint a \(\displaystyle DEF\) háromszög szögei \(\displaystyle \alpha,\beta,\gamma\). A szimmetria miatt feltehetjük, hogy \(\displaystyle \alpha\le\beta\le\gamma\), ekkor \(\displaystyle 90^\circ-\tfrac\gamma2\le90^\circ-\tfrac\beta2\le90^\circ-\tfrac\alpha2\), emiatt egyértelmű, hogy melyik szög melyik szöggel egyenlő: \(\displaystyle 90^\circ-\tfrac\gamma2=\alpha\), \(\displaystyle 90^\circ-\tfrac\beta2=\beta\) és \(\displaystyle 90^\circ-\tfrac\alpha2=\gamma\). A második egyenlőségből rögtön adódik, hogy \(\displaystyle 90^{\circ}=\frac32\beta\), vagyis \(\displaystyle \beta=60^{\circ}\). Az elsőből és a harmadikból pedig \(\displaystyle 90^{\circ}=\alpha+\frac{\gamma}{2}=\gamma+\frac{\alpha}{2}\), amiből \(\displaystyle \alpha/2/=\gamma/2\), azaz \(\displaystyle \alpha=\gamma\). Mivel \(\displaystyle \alpha+\gamma=180^{\circ}-\beta=120^{\circ}\), ebből már következik, hogy \(\displaystyle \alpha=\gamma=60^{\circ}\).

Tehát a feladatban szereplő háromszög mindhárom szöge \(\displaystyle 60^\circ\)-os, a háromszög szabályos.

Statistics:

144 students sent a solution.
5 points:	Albert Ákos, Balázs Réka, Bana Marcell, Bánó Bulcsú, Barczikay Ákos, Cserkuti Sándor, Domján Olivér, Feczkó Nóra, Fekete Patrik, Foris Dávid, Fórizs Botond, Gombos Gergely , Görömbey László, Hajós Balázs, Halász Henrik, Hegedűs András , Horváth Milán, Kalocsai Zoltán, Kocsis 827 Péter, Kovács Benedek Noel, Kun Timon, Kurucz Kitti, László Gergely, Lőw László, Márky Anna, Mátéfy Ádám , Metzger Ábris András, Nagy 989 Lea, Németh László Csaba, Németh Máté Előd, Perényi Lídia , Reviczki Roland, Sárvári Borka Luca, Sebestyén József Tas, Somogyi Dalma, Szabó 219 Petra, Szalanics Tamás, Szalay Réka, Szirmai Dénes, Téglás Panna.
4 points:	19 students.
3 points:	31 students.
2 points:	8 students.
1 point:	14 students.
0 point:	27 students.
Unfair, not evaluated:	5 solutionss.

Problems in Mathematics of KöMaL, October 2019