 |
A C. 1565. feladat (2019. október) |
C. 1565. Egy trapéz oldalai (valamilyen sorrendben) \(\displaystyle 2\), \(\displaystyle 3\), \(\displaystyle 5\), illetve \(\displaystyle 6\) egység hosszúak. Adjuk meg a területének lehető legnagyobb értékét.
(5 pont)
A beküldési határidő 2019. november 11-én LEJÁRT.
Megoldás. Alapvetően két gondolatmenetet alkalmaztak a versenyzők. Mindkettőben kihasználták, hogy a négy szakaszból \(\displaystyle \binom 42=6\)-féleképpen lehet kiválasztani az alapokat. (Mivel adott alapok esetén a szárak felcserélésével kapott két trapéz egybevágó, az így kapott két trapézt egy esetnek tekinthetjük.)
Az egyik út az volt, hogy megvizsgálták, melyik trapéz jön létre ezek közül. Erre két mód adódott: az egyik az 1. megoldásbeli, ahol az egyik szárat eltolva a keletkezett háromszöget vizsgálták a háromszög-egyenlőtlenség alapján. A másik út volt, hogy a trapézból két derékszögű háromszöget levágva a trapéz magasságát mindkét háromszögben felírt Pitagorasz-tétellel fejezték ki. Itt sokan elfeledkeztek arról, hogy mindhárom fajta trapézt megvizsgálják. (A hat eset egyikét ezzel a módszerrel vizsgálja meg a 2. megoldás.)
Gyakori hibás gondolatmenet volt a következő, aminek helyes változata a 2. megoldásban olvasható: Adott alapok esetén akkor kapjuk a legnagyobb területű trapézt, ha a magasság a lehető legnagyobb, vagyis – adott szakaszokról lévén szó – a rövidebb szár egyben magasság is. Ez alapján a hat esetből akkor lehetséges a lehető legnagyobb terület, ha az alapok 2, 3, a szárak 5, 6, és ebből az 5 hosszú szár merőleges az alapokra. Ekkor a terület \(\displaystyle \frac{(2+3)\cdot5}{2}=12,5\). De ha megnézzük az alábbi ábrán a keletkező \(\displaystyle EBC\) derékszögű háromszöget:
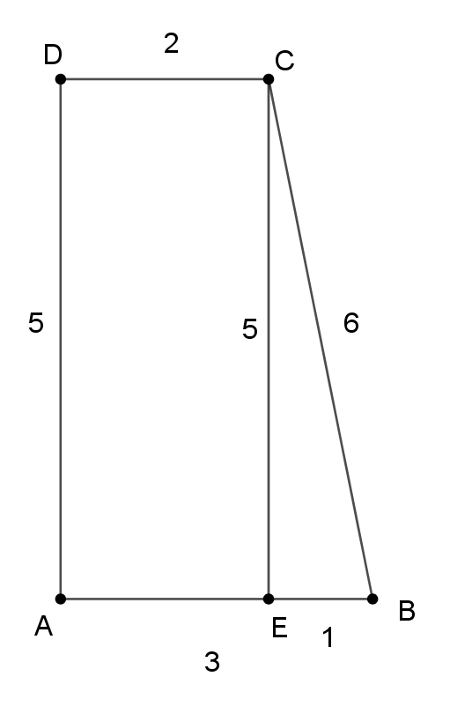
az átfogója egyenlő a befogójával, tehát nem jön létre (többen azt mutatták meg, hogy a Pitagorasz-tétel nem teljesül rá, tehát nem lehet derékszögű) – vagyis ez a trapéz valójában nem létezik.
A gondolatmenetben ott a hiba, hogy ez csak a lehetséges legnagyobb terület ezekkel az alapokkal. Attól még, hogy ez nem jön létre, lehet olyan eset, mikor nem merőleges egyik alap sem a szárra, de a terület még mindig nagyobb, mint 12, ami a következő lehetséges legnagyobb terület. A megoldás akkor teljes, ha belátjuk, hogy ilyen alapokkal és szárakkal nem létezik trapéz (vagy az 1., vagy a 2. megoldásban szereplő módon).
1. megoldás. Először is keressük meg,, hogy ilyen hosszúságú oldalakból egyáltalán milyen trapéz rakható össze. Legyenek a trapéz oldalai \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) és \(\displaystyle d\), ahol \(\displaystyle a\) jelöli a trapéz hosszabb alapját, \(\displaystyle c\) a másik alapot, és \(\displaystyle b\) a hosszabbik szár; a csúcsokat betűzzük az ábra szerint.
Ha a trapéz \(\displaystyle BC\) oldalát az \(\displaystyle AB\) oldallal párhuzamosan eltoljuk úgy, hogy a \(\displaystyle C\) pont a \(\displaystyle D\)-be kerüljön, akkor az \(\displaystyle ED\) szakaszt kapjuk. Ha \(\displaystyle BC>AD\), akkor a \(\displaystyle AED\) háromszög oldalai \(\displaystyle AE=a-c\), \(\displaystyle b'=b\) és \(\displaystyle d\). Ez a háromszög nem szerkeszthető, ha valamelyik oldalára nem teljesül a háromszög-egyenlőtlenség.
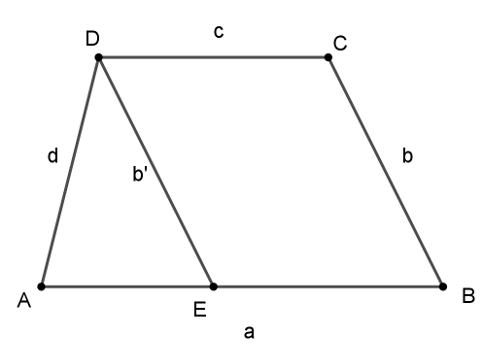
Az alábbi táblázat felsorolja az összes lehetséges esetet.
| \(\displaystyle a\) | \(\displaystyle c\) | \(\displaystyle a-c\) | \(\displaystyle b;d\) | Mi nem teljesül? |
| 2 | \(\displaystyle a\)-nak nagyobbnak kell lennie \(\displaystyle c\)-nél | |||
| 3 | 2 | 1 | 6;5 | \(\displaystyle 5=1+6\) |
| 5 | 2 | 3 | 6;3 | \(\displaystyle 6=3+3\) |
| 5 | 3 | 2 | 6;2 | \(\displaystyle 6>2+2\) |
| 6 | 2 | 4 | 5;3 | Mindhárom egyenlőtlenség teljesül |
| 6 | 3 | 3 | 5;2 | \(\displaystyle 5=3+2\) |
| 6 | 5 | 1 | 3;2 | \(\displaystyle 3=1+2\) |
Látjuk, hogy egyedül az \(\displaystyle a=6\), \(\displaystyle c=2\), \(\displaystyle b;d=3;5\) esetén létezik ilyen trapéz. Legyen \(\displaystyle b=3\) és \(\displaystyle d=5\) (a sorrend tetszőleges, hiszen a két trapéz egymás tükörképe).
Az \(\displaystyle AED\) háromszög oldalai tehát 3, 4 és 5, ami pitagoraszi számhármas, vagyis a háromszög derékszögű, és \(\displaystyle A\)-nál van a \(\displaystyle 90^{\circ}\)-os szöge. Ebből következik, hogy így a trapéz is derékszögű, vagyis a területe \(\displaystyle \frac{(a+c)\cdot d}{2}=12\).
Tehát beláttuk, hogy a trapéz területének lehető legnagyobb (és egyben egyetlen lehetséges) értéke 12.
Iván Petra (Budapest, Karinthy Frigyes Gimn., 11. évf.
2. megoldás. Megmutatjuk, hogy a terület lehető legnagyobb értéke 12. Ennyi lehet, tekintsük a következő esetet:
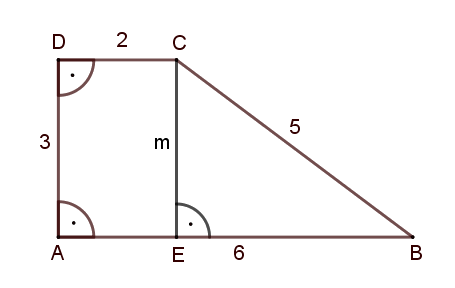
Vegyünk egy derékszögű trapézt, aminek két alapja 2 és 6 egység, derékszögeknél levő szára pedig 3. Ekkor a magassága is 3. Alkalmazva a Pitagorasz-tételt az \(\displaystyle EBC\) háromszögre (az ábra jelöléseit használva) kapjuk, hogy a másik szár 5 egység. Azaz ennek a trapéznak tényleg megfelelő hosszúságúak az oldalai és a területe \(\displaystyle \frac{(2+6)\cdot3}{2}=12\) egység.
Most vegyük észre, hogy bármely trapéz területére teljesül a következő egyenlőtlenség:
\(\displaystyle T \leq \frac{a+c}{2} \cdot \min(b,d),\)
ahol \(\displaystyle a\) és \(\displaystyle c\) a két alap. Hiszen az alapokhoz tartozó magasság kisebb vagy egyenlő a száraknál, mert a magasság, a szár és az alap egy része által akotott derékszögű háromszögben a szár átfogó, míg a magasság befogó (ha derékszögű a trapéz, akkor a derékszögnél lévő szárnál ez a háromszög elfajuló, a magasság egyenlő az egyik szárral).
A konkrét feladatban, ha \(\displaystyle \min(b,d)=2\), akkor
\(\displaystyle T \leq a+c \leq 11.\)
Ezekben az esetekben tehát biztosan 12-nél kisebb a terület.
Ha \(\displaystyle \min(b,d)=3\), akkor az egyik alap 2. Ekkor
\(\displaystyle T \leq \frac{2+6}{2} \cdot 3=12.\)
A megoldás elején adott konstrukció mutatja, hogy 12 tényleg lehet a terület. (Itt jegyezzük meg, hogy ebben az esetben – és mint később látni fogjuk összességében is – ez az egyetlen ilyen trapéz, aminek oldalai 2, 3, 5, 6 és területe 12. Hiszen az egyik alap 2, az egyik szár 3. A másik alapnak 6-nak kell lennie, hogy 12-t kapjunk területnek, a magasságnak pedig szintén 3-nak.)
Ha \(\displaystyle \min(b,d)=5\), akkor 2, 3 a két alap és 5, 6 a két szár hossza. Ekkor korábbi becslésünk túl gyenge:
\(\displaystyle T \leq \frac{25}{2},\)
ami nagyobb, mint 12. Csakhogy ilyen alapokkal és szárakkal nem is létezik trapéz. Tegyük fel ugyanis, hogy van ilyen trapéz:
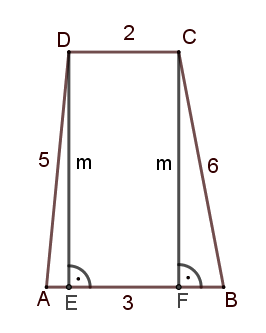
Fejezzük ki a trapéz magasságának négyzetét a Pitagorasz-tétel segítségével az \(\displaystyle AED\) és a \(\displaystyle BFC\) (esetleg elfajuló) derékszögű háromszögekben. Az ábrán az az eset látható, amikor az \(\displaystyle AB\) egyenesen a pontok sorrendje \(\displaystyle A,E,F,B\). Legyen \(\displaystyle AE=x\) (ekkor \(\displaystyle FB=1-x\), hiszen \(\displaystyle EF=2\)):
\(\displaystyle m^2= 25- x^2=36 - (1-x)^2,\)
\(\displaystyle 2x=-10, \)
\(\displaystyle x=-5.\)
Ez nem lehetséges.
Ha a \(\displaystyle B\) és az \(\displaystyle F\) sorrendje felcserélődne, vagyis a pontok sorrendje \(\displaystyle A,E,B,F\) akkor – mivel a 6 a hosszabb szár – \(\displaystyle AB\) rövidebb lenne \(\displaystyle CD\)-nél. Mivel ez nem így van, ezért ez nem lehetséges.
Ha az \(\displaystyle A\) és az \(\displaystyle E\) sorrendje cserélődik fel, és a pontok sorrendje \(\displaystyle E,A,F,B\), akkor \(\displaystyle AE=x\) miatt \(\displaystyle AF=2-x\) és \(\displaystyle FB=1+x\), a két Pitagorasz-tételből
\(\displaystyle m^2= 25- x^2=36 - (1+x)^2,\)
\(\displaystyle 2x=10, \)
\(\displaystyle x=5.\)
Mivel \(\displaystyle x\) nem lehet 2-nél nagyobb, ez sem lehetséges. (Előjeles szakaszokkal számolva, azaz eleve feltéve, hogy ha az \(\displaystyle A\) pont az \(\displaystyle EB\) szakaszon van, akkor \(\displaystyle x\) negatív, a két esetben ugyanazt az egyenletet kapjuk, de \(\displaystyle x=-5\) nem megoldás egyik esetben sem, hiszen ekkor az \(\displaystyle AED\) derékszögű háromszög befogója és átfogója is 5 lenne.)
Végül lehetséges a pontok \(\displaystyle E,F,A,B\) sorrendje is, ekkor \(\displaystyle FA=EA-EF=x-2\), \(\displaystyle FB=FA+AB=(x-2)+3=x+1\) és az egyenlet ugyanaz, mint az előbb, tehát ez sem ad megoldást.
Tehát beláttuk, hogy a trapéz területének lehető legnagyobb értéke 12.
Statisztika:
81 dolgozat érkezett. 5 pontot kapott: Bihari Petra, Biró Kinga, Csizmadia Máté Zalán, Farkas Jázmin, Fekete András Albert, Győri Gréta, Hajdú Bálint, Horváth 008 László, Iván Petra, Izsa Regina Mária, Kadem Aziz, Kalmár Dóra, Kis 194 Károly, Majerusz Ádám, Molnár 203 Bálint, Molnár Réka, Nagy 009 Dávid, Oláh 492 Emese, Palencsár Enikő, Pásti Bence, Ráduly Nóra Julianna, Rassai Erik, Schenk Anna, Schneider Anna, Sümegi Géza, Szabó Barbara Noémi, Szigeti Donát, Tápai Valér, Tölgyes Viktória, Trombitás Karolina Sarolta, Zaránd Andris. 4 pontot kapott: Arató Zita, Biró 424 Ádám, Danó Ádám, Egerszegi Balázs, Féger Tamás, Gál Bence, Glavosits Villő, Gombocz Péter, Harcsa-Pintér András, Kinyó Kincső, Ladányi Dániel, Ludányi Levente, Molnár Kristóf András, Molnár Nóra, Nagy Bálint Zoltán, Németh Kristóf, Rokonay Szonja, Székelyhidi Klára, Szin Imola. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 5 versenyző. 1 pontot kapott: 11 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 4 dolgozat.
A KöMaL 2019. októberi matematika feladatai

