 |
A C. 1570. feladat (2019. november) |
C. 1570. Egy hatszög minden szöge \(\displaystyle 120^{\circ}\), szemközti csúcsait összekötő átlói egyenlő hosszúak. Igazoljuk, hogy a hatszög forgásszimmetrikus.
Javasolta: Fried Katalin (Budapest)
(5 pont)
A beküldési határidő 2019. december 10-én LEJÁRT.
Megoldás. Egészítsük ki a hatszögünket egy háromszöggé minden második oldalának a meghosszabbításával az ábrán látható módon, és használjuk mostantól az ábra jelöléseit. Ez a háromszög szabályos, hiszen minden szöge \(\displaystyle 60^\circ\), mert a hatszögnek minden szöge \(\displaystyle 120^\circ\). Legyen 1 az \(\displaystyle ABC\) háromszög oldalhossza, \(\displaystyle d\) a hatszög feladatban szereplő átlóinak a hossza.
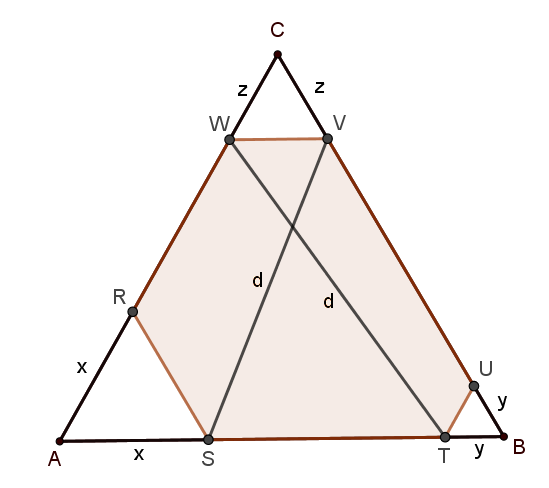
Ha \(\displaystyle x=y=z\), akkor a feladat feltételei teljesülnek, és a hatszög forgásszimmetrikus (\(\displaystyle 120^\circ\)-os, középpontja az \(\displaystyle ABC\) háromszög középpontja).
Most megmutatjuk, hogy a feladat feltéleinek eleget tevő hatszögre \(\displaystyle x=y=z\).
1. módszer. Az \(\displaystyle STVW\) trapéz átlói egyenlők, így a trapéz szimmetrikus. Ekkor pedig a két alap felező merőlegese egybeesik. Mivel a \(\displaystyle WV\) szakasz felező merőlegese átmegy az \(\displaystyle AB\) oldal felezőpontján, ezért ez a felezőpont egyben az \(\displaystyle ST\) szakasz felezőpontja. Tehát az \(\displaystyle S\) és a \(\displaystyle T\) pont az \(\displaystyle AB\) szakasz felezőpontjára szimmetrikusan helyezkednek el, amiből következik, hogy \(\displaystyle x=y\).
A \(\displaystyle VRSU\) trapézból kiindulva hasonló gondolatmenettel kapjuk, hogy \(\displaystyle y=z\).
Tehát \(\displaystyle x=y=z\), a hatszög forgásszimmetrikus.
2. módszer. Jegyezzük meg, hogy \(\displaystyle x+y, y+z, x+z <1\), valamint legyen \(\displaystyle 1-x=:X, 1-y=:Y, 1-z=:Z\). Írjuk fel a koszinusztételt az \(\displaystyle SBV\), majd az \(\displaystyle ATW\) háromszögre:
\(\displaystyle X^2+Z^2-2XZ\cos60^\circ=d^2,\)
\(\displaystyle Y^2+Z^2-2YZ\cos60^\circ=d^2.\)
Tehát
\(\displaystyle X^2+Z^2-XZ=d^2,\)
\(\displaystyle Y^2+Z^2-YZ=d^2.\)
Ebből a két egyenlet bal oldalai egyenlők:
\(\displaystyle X^2+Z^2-XZ=Y^2+Z^2-YZ,\)
amit átalakítva és nullára rendezve kapjuk, hogy
\(\displaystyle (X-Y)(X+Y-Z)=0.\)
Egy szorzat pontosan akkor 0, ha valamelyik tényezője 0, azaz
vagy \(\displaystyle X-Y=0\), amiből \(\displaystyle X=Y\)
vagy \(\displaystyle X+Y-Z=0\), amiből \(\displaystyle 1-x+1-y=1-z\), azaz \(\displaystyle 1=x+y-z\), de ez nem lehetséges, mert \(\displaystyle x+y-z<1-z<1\).
Hasonlóan belátható, hogy \(\displaystyle X=Z\) is teljesül, azaz kaptuk, hogy \(\displaystyle X=Y=Z\). Ebből következik, hogy \(\displaystyle x=y=z\).
Tehát beláttuk, hogy az összes feladat feltételeinek eleget tevő hatszögre \(\displaystyle x=y=z\), vagyis a hatszög forgásszimmetrikus.
Statisztika:
183 dolgozat érkezett. 5 pontot kapott: Cserkuti Sándor, Csilling Dániel, Csonka Illés, Dékány Csaba, Egyházi Hanna, Feczkó Nóra, Halász Henrik, Horváth Milán, Inokai Dávid, Kalabay László, Kalocsai Zoltán, Király Előd István, Kovács Benedek Noel, Lőw László, Metzger Ábris András, Mócsy Mátyás, Nagy 989 Lea, Palencsár Enikő, Schneider Anna, Somogyi Dalma, Téglás Panna, Zaránd Andris. 4 pontot kapott: Barát Benedek, Féger Tamás, Hajós Balázs, Kis 194 Károly, Mátéfy Ádám , Mihalik Bálint, Rátki Gergely, Szalanics Tamás, Trombitás Karolina Sarolta. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 13 versenyző. 1 pontot kapott: 97 versenyző. 0 pontot kapott: 34 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2019. novemberi matematika feladatai

