Problem C. 1572. (November 2019)

C. 1572. In a trapezium \(\displaystyle ABCD\), let \(\displaystyle M\) denote the intersection of diagonals \(\displaystyle AC\) and \(\displaystyle BD\), and let \(\displaystyle N\) and \(\displaystyle P\) denote the centres of the circumscribed circles of triangles \(\displaystyle ABC\) and \(\displaystyle ACD\), respectively. Prove that \(\displaystyle M\), \(\displaystyle N\) and \(\displaystyle P\) are collinear if and only if \(\displaystyle ABCD\) is a parallelogram or a cyclic trapezium.

(5 pont)

Deadline expired on December 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Feltehető, hogy \(\displaystyle AB\) és \(\displaystyle CD\) a trapéz alapjai (hiszen az \(\displaystyle ABC\) és \(\displaystyle ACD\) háromszögeket úgy kapjuk, hogy a trapéz egyik csúcsához a másik három közül két-két szomszédosat veszünk hozzá).

Először vegyük észre, hogy \(\displaystyle N\) is és \(\displaystyle P\) is rajta van az \(\displaystyle AC\) oldalfelező merőlegesén, hiszen bármely háromszög körülírt körének középpontja az oldalak felezőmerőlegeseinek a metszéspontja.

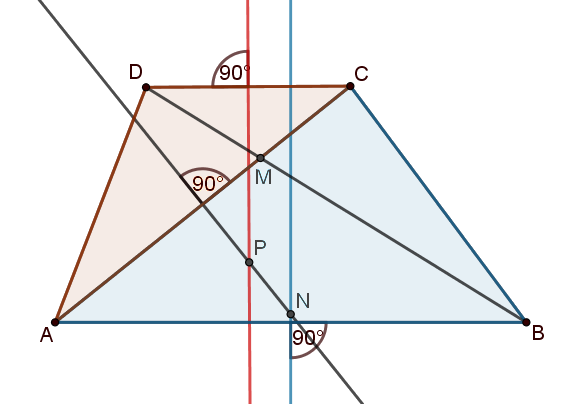
I. Először tegyük fel, hogy \(\displaystyle M\), \(\displaystyle N\) és \(\displaystyle P\) egy egyenesre esik. Ekkor két eset lehetséges:

1. \(\displaystyle N\) és \(\displaystyle P\) két különböző pont

Ilyenkor az \(\displaystyle NP\) egyenes nem más, mint \(\displaystyle AC\) oldalfelező merőlegese. Ekkor \(\displaystyle M\)-nek is rajta kell lennie ezen az egyenesen, így mivel rajta van \(\displaystyle AC\) átlón is, ezért \(\displaystyle M\) az \(\displaystyle AC\) átló felezőpontja. Ekkor \(\displaystyle M\) a \(\displaystyle BD\) átló felezőpontja is, hiszen bármely trapézban az átlók felezőpontjai rajta vannak a trapéz középvonalán, így ha az egyik átló felezi a másikat, akkor ,,a másik is az egyiket''. Tehát \(\displaystyle ABCD\) olyan trapéz, aminek az átlói felezik egymást, azaz paralelogramma.

2. \(\displaystyle N\) és \(\displaystyle P\) egybeesik

Mivel \(\displaystyle N\) az \(\displaystyle ABC\), \(\displaystyle P\) pedig az \(\displaystyle ACD\) körülírt körének középpontja, ezért \(\displaystyle N=P\) esetén a két körülírt kör egybeesik, vagyis \(\displaystyle ABCD\) húrtrapéz.

II. Most igazoljuk a másik irányt, azaz tegyük fel, hogy \(\displaystyle ABCD\) trapéz paralelogramma vagy húrtrapéz.

1. eset: Az \(\displaystyle ABCD\) trapéz paralelogramma

Ekkor \(\displaystyle M\) felezi az \(\displaystyle AC\) átlót, azaz rajta van \(\displaystyle AC\) oldalfelező merőlegesén, amire illeszkedik \(\displaystyle N\) és \(\displaystyle P\) is, így \(\displaystyle M\), \(\displaystyle N\) és \(\displaystyle P\) valóban egy egyenesre esnek.

2. eset: Az \(\displaystyle ABCD\) trapéz húrtrapéz

Ekkor az \(\displaystyle ABCD\) húrtrapéz köré írható kör középpontja \(\displaystyle N=P\). Így természetesen \(\displaystyle M\) és \(\displaystyle N=P\) egy egyenesre esnek.

Statistics:

40 students sent a solution.
5 points:	Gál Bence, Hajdú Bálint, Kis 194 Károly, Lakatos Enikő, Molnár Réka, Zaránd Andris.
4 points:	Izsa Regina Mária, Ludányi Levente.
3 points:	15 students.
2 points:	10 students.
1 point:	5 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, November 2019