Problem C. 1576. (December 2019)

C. 1576. A unit circle is centred at \(\displaystyle O\), and \(\displaystyle P\) is a point such that \(\displaystyle OP=2\). Consider a secant through \(\displaystyle P\) that intersects the circle at points \(\displaystyle M\) and \(\displaystyle N\) such that \(\displaystyle M\) bisects the line segment \(\displaystyle NP\). Prove that the area of triangle \(\displaystyle OMN\) is smaller than \(\displaystyle \frac{1}{2}\).

(5 pont)

Deadline expired on January 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Az \(\displaystyle OMN\) háromszög egyenlőszárú, hiszen \(\displaystyle OM=ON=1\). Legyen az \(\displaystyle O\)-ból induló magasságának talppontja \(\displaystyle T\). Ekkor \(\displaystyle TM=TN=MN/2.\)

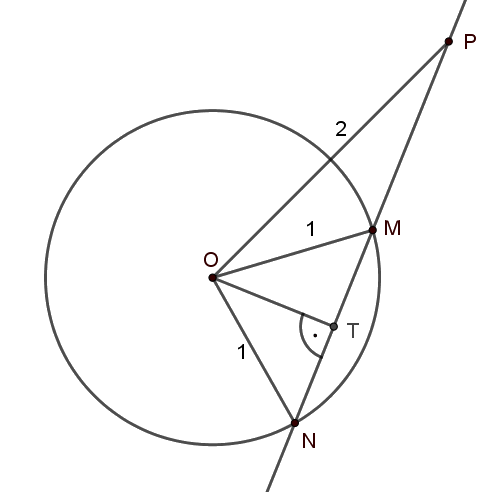
A \(\displaystyle P\) pont a feladatban szereplő körre vonatkozó hatványa \(\displaystyle OP^2-1^2=3\), amivel egyenlő a szelőszakaszok hosszának szorzata, azaz

\(\displaystyle PM \cdot PN = 3.\)

Mivel \(\displaystyle M\) felezőpontja \(\displaystyle PN\)-nek, így \(\displaystyle 2PM=PN\), azaz

\(\displaystyle 2 PM^2=3.\)

Ebből \(\displaystyle PM=\sqrt{\frac{3}{2}}\), és így \(\displaystyle MN\) is \(\displaystyle \sqrt{\frac{3}{2}}\).

Most számoljuk ki az \(\displaystyle OMN\) háromszög \(\displaystyle OT\) magasságát. Alkalmazzuk a Pitagorasz-tételt az \(\displaystyle OTM\) háromszögre:

\(\displaystyle OT= \sqrt{1^2-\left(\frac{\sqrt{\frac{3}{2}}}{2}\right)^2} =\sqrt{\frac{5}{8}}. \)

Ebből az \(\displaystyle OMN\) háromszög területe:

\(\displaystyle T= \frac{\sqrt{\frac{3}{2}} \cdot \sqrt{\frac{5}{8}}}{2}= \sqrt{\frac{15}{64}} < \frac{1}{2}.\)

2. megoldás. A feltétel szerint az \(\displaystyle ONP\) háromszögben \(\displaystyle OM\) súlyvonal, így az \(\displaystyle OMN\) háromszög területe fele az \(\displaystyle ONP\) háromszög területének. Az \(\displaystyle ONP\) háromszög területe pedig kisebb, mint 1, hiszen \(\displaystyle OP=2\) és a hozzá tartozó magasság kisebb 1-nél, a kör sugaránál. Ezen utóbbihoz elég megmutatni, hogy a \(\displaystyle PON\) szög nem lehet derékszög (a körvonalon lévő \(\displaystyle N\) pont csak így lehetne 1 távolságra a középponton átmenő \(\displaystyle OP\) egyenestől). Tegyük fel indirekten, hogy a \(\displaystyle PON\) szög derékszög. Ekkor a Thalész-tétel megfordítása szerint \(\displaystyle 1=MO=MN=MP\), amiből az \(\displaystyle OMP\) háromszögben \(\displaystyle OP=OM+MP\), ez pedig a háromszög-egyenlőtlenség miatt nem lehetséges.

Tehát \(\displaystyle OMN\) háromszög területe kisebb \(\displaystyle 1/2\)-nél.

Statistics:

194 students sent a solution.
5 points:	125 students.
4 points:	16 students.
3 points:	26 students.
2 points:	15 students.
1 point:	10 students.
0 point:	1 student.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, December 2019