 |
A C. 1588. feladat (2020. február) |
C. 1588. Legyenek az \(\displaystyle ABCD\) négyszög \(\displaystyle AB\), illetve \(\displaystyle AD\) oldalainak \(\displaystyle A\)-hoz közelebbi harmadolópontjai \(\displaystyle E\) és \(\displaystyle F\), a \(\displaystyle BC\) oldal \(\displaystyle B\)-hez közelebbi harmadolópontja pedig \(\displaystyle G\). Tükrözzük a \(\displaystyle G\) pontot \(\displaystyle E\)-re, majd az így kapott tükörképet \(\displaystyle F\)-re. Igazoljuk, hogy a kapott tükörkép ráesik a négyszög valamely oldalára. Melyik oldalon van, és milyen arányban osztja azt?
(5 pont)
A beküldési határidő 2020. március 10-én LEJÁRT.
Megoldás. Legyen a \(\displaystyle G\) pont tükörképe az \(\displaystyle E\)-re vonatkozó tükrözés után \(\displaystyle G'\), majd ennek a pontnak az \(\displaystyle F\)-re vonatkozó tükörképe \(\displaystyle G''\) az ábrán is látható módon. Továbbá legyen \(\displaystyle H\) a \(\displaystyle DC\) oldal \(\displaystyle D\)-hez közelebbi harmadolópontja.
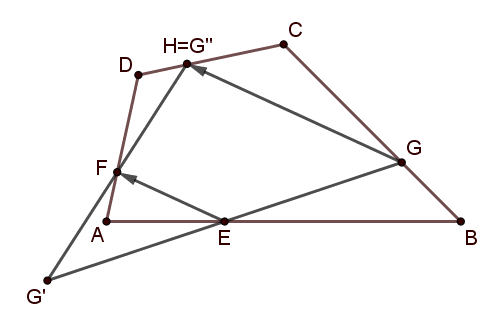
Megmutatjuk, hogy \(\displaystyle G''=H\), azaz \(\displaystyle G''\) a \(\displaystyle DC\) oldalon van, éspedig annak \(\displaystyle D\)-hez közelebbi harmadolópontja.
Először is, ismert, hogy az \(\displaystyle E\)-re, majd \(\displaystyle F\)-re vonatkozó egymás utáni középpontos tükrözés nem más mint a \(\displaystyle 2\overrightarrow{EF}\) vektorral történő eltolás. Így \(\displaystyle \overrightarrow{GG''}=2\overrightarrow{EF}\).
Tudjuk, hogy \(\displaystyle H\) a \(\displaystyle CD\) oldal \(\displaystyle D\)-hez közelebbi harmadolópontja, \(\displaystyle G\) pedig a \(\displaystyle BC\) oldal \(\displaystyle B\)-hez közelebbi harmadolópontja, így \(\displaystyle \frac{CH}{CD}=\frac{CG}{CB}=\frac23\). A \(\displaystyle DCB\) szögre alkalmazva a párhuzamos szelőszakaszok tételének megdordítását kapjuk, hogy \(\displaystyle GH \parallel BD\) és \(\displaystyle GH=\frac23 BD\). Hasonlóan, a \(\displaystyle BAD\) szöget nézve \(\displaystyle EF \parallel BD\) és \(\displaystyle EF=\frac13 BD\). Ezekből következik, hogy \(\displaystyle \overrightarrow{GH}=\frac23\overrightarrow{BD}=2\overrightarrow{EF}\).
Mivel \(\displaystyle \overrightarrow{GG''}=2\overrightarrow{EF}=\overrightarrow{GH}\), ezért \(\displaystyle G''=H\), azaz megmutattuk, hogy \(\displaystyle G''\) rajta van a \(\displaystyle CD\) oldalon, méghozzá annak \(\displaystyle D\)-hez közelebbi harmadolópontja.
Statisztika:
93 dolgozat érkezett. 5 pontot kapott: Albert Ákos, Barczikay Ákos, Blázsik Árpád, Cserkuti Sándor, Csilling Dániel, Csonka Illés, Dékány Csaba, Domján Olivér, Egyházi Hanna, Erős 135 Milán, Feczkó Nóra, Gombos Gergely , Hamar János, Inokai Dávid, Kalocsai Zoltán, Lőw László, Mészáros Anna Veronika, Németh László Csaba, Pilz Olivér, Sipos Teodor, Somogyi Dalma, Stein Felix, Szabó Réka, Szabó Zóra, Szakács Domonkos, Szalanics Tamás, Szalay Réka, Varga 128 Erik. 4 pontot kapott: Baksay Réka, Császár Boglárka, Dancsó 172 Dorottya, Domokos Lóránt, Flódung Áron , Hajós Balázs, Horváth Milán, Koczkás Árpád, Koleszár Domonkos, Kovács Ádám Martin, Novák Zalán Zoltán, Pesti Patrik, Rács Zsóka, Téglás Panna, Varga Boldizsár, Vincze Dorka. 3 pontot kapott: 12 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 9 versenyző. 0 pontot kapott: 10 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2020. februári matematika feladatai

