A C. 1596. feladat (2020. március)

C. 1596. Egy háromszög oldalai 5 cm, 5 cm és 6 cm hosszúak. A háromszögbe írható körnek az oldalakkal párhuzamos érintői és az oldalak egy hatszöget zárnak közre. Mekkora ennek a területe?

(5 pont)

A beküldési határidő 2020. április 14-én LEJÁRT.

Megoldás. A megoldás során a rövidebb írásmód kedvéért a cm mértékegységet nem tüntetjük fel, egy egységnek a jelentése 1 cm lesz.

Használjuk az ábra jelöléseit: Legyenek a háromszög csúcsai \(\displaystyle A, B, C\) (\(\displaystyle AB=6, AC=BC=5\)), a keletkező hatszög csúcsai pedig \(\displaystyle L,M, N, O, P, Q\). A beírt kör sugara \(\displaystyle r\), a \(\displaystyle C\) csúcsból induló magasság talppontja \(\displaystyle E\), az \(\displaystyle OP\) szakaszon az érintési pont \(\displaystyle K\). (A tengelyes szimmetria alapján \(\displaystyle E\) egyben az \(\displaystyle AB\) oldal felezőpontja és a beírt kör érintési pontja, \(\displaystyle K\) pedig a beírt körön az \(\displaystyle E\)-vel átellenes pont.)

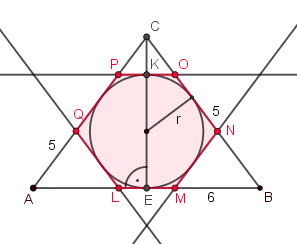
A Pitagorasz-tétel alapján a \(\displaystyle CE\) magasság hossze \(\displaystyle CE=\sqrt{BC^2-BE^2}=\sqrt{5^2-3^2}=4\), így az \(\displaystyle ABC\) háromszög területe

\(\displaystyle T=\frac{AB\cdot CE}{2}=\frac{6\cdot 4}{2}=12.\)

Most írjuk fel a területet a félkerület (\(\displaystyle s=8\)) és a beírt kör sugara segítségével:

\(\displaystyle T= r \cdot s, \)

\(\displaystyle 12= r \cdot 8,\)

amiből

\(\displaystyle r=\frac32.\)

Mivel \(\displaystyle OP\) egyenes párhuzamsos \(\displaystyle AB\)-vel, így \(\displaystyle POC\) háromszög hasonló \(\displaystyle ABC\) háromszöghöz. Meghatározva a hasonlóság arányát, tudni fogjuk \(\displaystyle POC\) háromszög területét is (a hasonlóság arányának négyzete lesz a területek aránya).

Korábban már meghatároztuk, hogy \(\displaystyle EC= 4\), a \(\displaystyle POC\) háromszög \(\displaystyle CK\) magassága pedig

\(\displaystyle CK=EC-2r=4-3=1.\)

Azaz a két háromszög magasságának aránya \(\displaystyle 1:4\), azaz a területük aránya \(\displaystyle 1:16\). Ebből

\(\displaystyle T_{POC}=\frac{12}{16}=\frac{3}{4}.\)

Szimmetriai okokból \(\displaystyle ALQ\) és \(\displaystyle MBN\) háromszög területe egyenlő, és hasonló módon számolható ki, mint \(\displaystyle POC\) háromszög területe. Például, nézzük az \(\displaystyle ALQ\) háromszöget. Az \(\displaystyle ABC\) háromszögben a \(\displaystyle BC\) oldalhoz tartozó magasság hossza \(\displaystyle \frac{24}{5}\). Az \(\displaystyle ALQ\) háromszögben a \(\displaystyle QL\)-hez tartozó magasság hossza \(\displaystyle \frac{24}{5}-2r=\frac{24}{5}-3=\frac{9}{5}\). Azaz a két háromszög hasonlóságának aránya \(\displaystyle (9/5):(24/5)=3:8\), így a területük aránya \(\displaystyle 9:64\). Ebből

\(\displaystyle T_{ALQ}=12 \cdot \frac{9}{64}= \frac{27}{16}.\)

Ekkor a hatszög területét már ki tudjuk számolni úgy, hogy az \(\displaystyle ABC\) háromszög területéből kivonjuk a három ,,kis'' háromszög területét:

\(\displaystyle T_{\text{hatszög}}=12-\frac34-2 \cdot \frac{27}{16}= \frac{63}{8}.\)

Tehát a hatszög területe \(\displaystyle \frac{63}{8}\ \text{cm}^2\).

Statisztika:

103 dolgozat érkezett.
5 pontot kapott:	Bánó Bulcsú, Cseke Balázs, Cserkuti Sándor, Deák Gergely, Egyházi Hanna, Feczkó Nóra, Fekete Patrik, Hajós Balázs, Horváth Milán, Kalocsai Zoltán, Kruppa László, László Gergely, Lőw László, Mészáros Anna Veronika, Nagy 429 Leila, Németh László Csaba, Sárvári Borka Luca, Schiller Bence, Szabó 219 Petra, Szabó 423 Ágnes, Szabó Réka, Szabó Zóra, Szász Csenge, Szélpál Petra, Szirmai Dénes, Üveges Laura , Veres Dorottya.
4 pontot kapott:	Bányai Kristóf, Barát Benedek, Csilling Dániel, Csonka Illés, Domján Olivér, Dózsa Levente, Fonyódi Sára, Gombos Dóra, Gombos Gergely , Héjja Márton, Horváth Antal, Mátéfy Ádám , Nagy 989 Lea, Szakács Domonkos, Szittyai Anna, Téglás Panna.
3 pontot kapott:	17 versenyző.
2 pontot kapott:	30 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2020. márciusi matematika feladatai