 |
A C. 1598. feladat (2020. március) |
C. 1598. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle AB\) és \(\displaystyle CD\) oldalainak felezőpontjait összekötő \(\displaystyle MN\) szakasz hossza az \(\displaystyle AD\) és \(\displaystyle BC\) oldalak hosszának számtani közepe. Mutassuk meg, hogy az \(\displaystyle ABCD\) négyszög trapéz.
(5 pont)
A beküldési határidő 2020. április 14-én LEJÁRT.
Megoldás. Az \(\displaystyle ABCD\) négyszöget tükrözzük középpontosan az \(\displaystyle AB\) oldal \(\displaystyle M\) felezőpontjára, a képpontokat jelöljük a szokásos módon az ábrán is látható módon: \(\displaystyle X\) képe \(\displaystyle X'\).
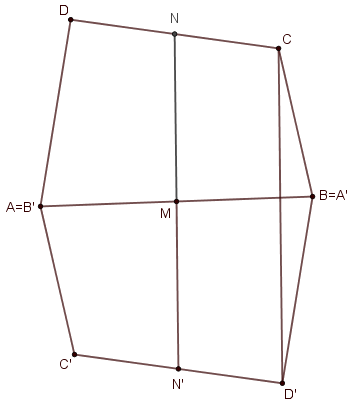
Mivel \(\displaystyle N\) a \(\displaystyle CD\) oldal felezőpontja, ezért \(\displaystyle NC=ND\). A középpontos tükrözés tulajdonságai miatt \(\displaystyle ND=N'D'\) és \(\displaystyle ND \parallel N'D'\). Így \(\displaystyle NC\) és \(\displaystyle N'D'\) párhuzamos és egyenlő hosszú, azaz \(\displaystyle N'D'CN\) négyszög paralelogramma. Emiatt \(\displaystyle NN'\) és \(\displaystyle CD'\) is párhuzamos és egyenlő hosszú.
Másrészről \(\displaystyle NN'=2 \cdot MN = BC+AD\). Így \(\displaystyle CD'=NN'=BC+AD\). Továbbá \(\displaystyle AD=A'D'(=BD')\) a középpontos tükrözés tulajdonságai miatt. Így a \(\displaystyle CD'B\) háromszögben két oldal összege pont a harmadik oldal (\(\displaystyle CD'=BC+BD'\)), azaz ez egy elfajuló háromszög, \(\displaystyle B\) rajta van \(\displaystyle CD'\) egyenesen. Emiatt \(\displaystyle CB \parallel MN\).
Ugyanígy igazolható \(\displaystyle AD\)-ről is, hogy párhuzamos \(\displaystyle MN\)-nel, emiatt \(\displaystyle AD \parallel BC\), azaz \(\displaystyle ABCD\) négyszög valóban trapéz.
Statisztika:
95 dolgozat érkezett. 5 pontot kapott: Amaan Khan, Ámmer Fanni, Arató Zita, Barát Benedek, Barczikay Ákos, Biró 424 Ádám, Buzás Bence István, Cserkuti Sándor, Csonka Illés, Czehlár Gergely, Deák Gergely, Egyházi Hanna, Feczkó Nóra, Féger Tamás, Fekete Patrik, Hajdú Bálint, Halász Henrik, Horváth Antal, Horváth Milán, Kalabay László, Kalocsai Zoltán, Koleszár Domonkos, Lukács Emma, Majerusz Ádám, Metzger Ábris András, Molnár Réka, Németh László Csaba, Nyári Péter Ádám, Palencsár Enikő, Rács Zsóka, Schneider Anna, Sebestyén József Tas, Somogyi Dalma, Stein Felix, Szabó Réka, Szakács Domonkos, Szalanics Tamás, Trombitás Karolina Sarolta, Varga Boldizsár, Xu Yiling, Zaránd Andris. 4 pontot kapott: 16 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 13 versenyző. 0 pontot kapott: 15 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2020. márciusi matematika feladatai

