 |
A C. 1601. feladat (2020. március) |
C. 1601. Egy szabályos négyoldalú gúla oldallapjának magassága kétszerese az alaplap élének. Az alaplap síkjától számítva a magasság hány százalékánál kell az alaplap síkjával párhuzamosan kettévágni a gúlát ahhoz, hogy a keletkezett csonkagúla palástjának és fedőlapjának területe összesen pont fele legyen az eredeti gúla palástja területének?
(5 pont)
A beküldési határidő 2020. április 14-én LEJÁRT.
Megoldás. A gúla alapélének hossza legyen \(\displaystyle a\), ekkor az oldallapok magassága \(\displaystyle 2a\). Nézzünk egy oldallapot. Mikor a gúlát az alaplappal párhuzamos síkkal kettévágjuk, akkor egy oldallapot az alapéllel párhuzamos szakasszal – a sík és az oldallap metszete – kettévágunk egy háromszögre és egy trapézra az ábrán látható módon. Az oldallap csúcsai legyenek \(\displaystyle A, B, E\), és a szakasz végpontjai \(\displaystyle J, K\) (az ábra szerint).
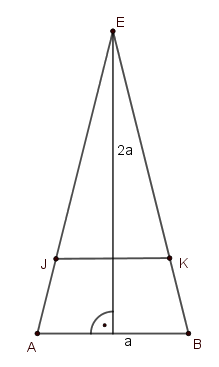
Az \(\displaystyle ABE\) háromszög hasonló \(\displaystyle JKE\) háromszöghöz (két oldaluk egy egyenesen van, a harmadik párhuzamos), a hasonlóság aránya legyen \(\displaystyle \lambda\). Ekkor a területük aránya \(\displaystyle \lambda^2\), továbbá \(\displaystyle JK=\lambda a\).
\(\displaystyle T_{ABE}= \frac{2a \cdot a}{2}= a^2,\)
ekkor
\(\displaystyle T_{JKE}= \lambda^2 a^2.\)
Így az \(\displaystyle ABJK\) trapéz területe
\(\displaystyle T_{ABJK}= (1-\lambda^2)a^2.\)
Az eredeti gúla palástjának területe négyszerese az \(\displaystyle ABE\) oldallap háromszög területének (hiszen a gúla szabályos):
\(\displaystyle T_{\text{palást}}=4 a^2.\)
Így a csonkagúla fedőlapjának (\(\displaystyle \lambda a\) oldalú négyzet) és palástjának összterületének \(\displaystyle 2 a^2\)-nek kell lennie. (A korábbiak szerint a csonkagúla palástja 4 db egybevágó trapézból áll, melyek területe megegyezik \(\displaystyle ABJK\) területével.)
\(\displaystyle T=2 a^2= (\lambda a )^2 + 4 (1-\lambda^2)a^2,\)
\(\displaystyle 2a^2= 4 a^2 - 3 \lambda^2a^2,\)
amiből
\(\displaystyle \lambda^2= \frac23,\)
vagyis
\(\displaystyle \lambda = \sqrt{\frac23}.\)
Ebből \(\displaystyle 1-\lambda= 1-\sqrt{\frac23} \approx 0,1835. \)
Azaz a magasság \(\displaystyle \left(1-\sqrt{\frac23}\right) \cdot 100 \approx 18,35 \% \)-ánál kell elvágni a gúlát. (Ez persze mind a gúla magasságára, minden az oldallap magasságára is igaz.)
Statisztika:
41 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Antal Virág Anna, Biró 424 Ádám, Buzás Bence István, Hajdú Bálint, Izsa Regina Mária, Kelemen Anna, Kis 194 Károly, Kosóczki Balázs, Kulcsár Kevin, Molnár Réka, Nagy 009 Dávid, Nyári Péter Ádám, Palencsár Enikő, Rátki Gergely, Rosta Benjamin, Szabó Csege, Székelyhidi Klára, Szigeti Donát, Vakaris Klyvis. 4 pontot kapott: Ámmer Fanni, Arató Zita, Féger Tamás, Fekete András Albert, Lukács Emma, Nagy Vanda Orsolya, Németh Kristóf, Pál Mihály, Schneider Anna, Sümegi Géza, Trombitás Karolina Sarolta, Tüske Anna, Viharos Márta Judit. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2020. márciusi matematika feladatai

