 |
A C. 1603. feladat (2020. április) |
C. 1603. Az \(\displaystyle ABC\) egyenlőszárú háromszög \(\displaystyle A\) csúcsából induló magasságvonal a \(\displaystyle BC\) szárt \(\displaystyle T\)-ben metszi, a magasságpontot jelölje \(\displaystyle M\), a beírt körének középpontját pedig \(\displaystyle O\). Bizonyítsuk be, hogy ha az \(\displaystyle OT\) egyenes párhuzamos az \(\displaystyle AB\) alappal, akkor \(\displaystyle MC=2AM\).
(5 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. Legyen \(\displaystyle D\) a \(\displaystyle C\) csúcsból induló magasság talppontja, ezen rajta van \(\displaystyle O\) is, hiszen \(\displaystyle ABC\) háromszög egyenlő szárú és az alaphoz tartozó magasságvonal egyben szögfelezője is az alappal szemközti szögnek. \(\displaystyle T\)-ből állítsunk merőlegest \(\displaystyle AB\)-re, talppontja legyen \(\displaystyle F\), valamint \(\displaystyle O\)-ból a \(\displaystyle BC\) szárra állított merőleges talppontját jelölje \(\displaystyle E\). Az ábrán az így keletkező derékszögeket zölddel jelöltük.
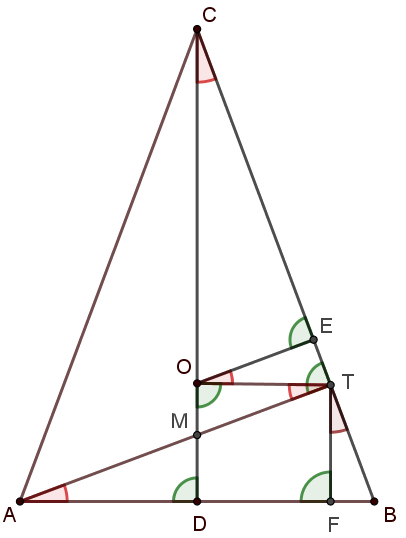
Továbbá a párhuzamos és merőleges szakaszok miatt \(\displaystyle BAT \angle = FTB \angle = ATO \angle = TOE \angle = ECO \angle\), ezeket pirossal jelöltük.
Először vegyük észre, hogy \(\displaystyle OD=OE\), mert mindkettő a beírt kör sugarával egyenlő, továbbá \(\displaystyle OD=FT\), mert a \(\displaystyle DFTO\) négyszög téglalap. Azaz
\(\displaystyle OE=OD=FT.\)
Emiatt az \(\displaystyle FBT\) és az \(\displaystyle ETO\) derékszögű háromszögek egybevágóak, mert egyik befogójuk és szögeik megegyeznek. Tehát
\(\displaystyle BT=TO.\)
Ebből következően az \(\displaystyle ABT\) és a \(\displaystyle CTO\) háromszögek is egybevágóak, hiszen szögeik és egyik befogójuk egyenlő. Tehát
\(\displaystyle CT=AB=2AD.\)
Végül a \(\displaystyle CMT\) ás \(\displaystyle AMD\) háromszögek hasonlók, mert szögeik megegyeznek, így
\(\displaystyle \frac{AM}{CM}= \frac{AD}{CT}=\frac{1}{2},\)
tehát
\(\displaystyle CM=2AM,\)
azaz az állítást beláttuk.
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Cserkuti Sándor, Csilling Dániel, Csonka Illés, Egyházi Hanna, Feczkó Nóra, Hajós Balázs, Horváth Milán, Kalocsai Zoltán, Kovács Benedek Noel, László Gergely, Németh László Csaba, Somogyi Dalma, Szabó Zóra, Szalanics Tamás, Szamkó Szabolcs, Téglás Panna. 4 pontot kapott: Barát Benedek, Fekete Patrik, Foris Dávid, Nagy 429 Leila, Németh Máté Előd, Sebestyén József Tas, Varga Boldizsár. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 4 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. áprilisi matematika feladatai

