 |
A C. 1605. feladat (2020. április) |
C. 1605. Az \(\displaystyle ABCD\) konvex négyszög átlóinak metszéspontja \(\displaystyle M\). Az \(\displaystyle ABM\) háromszög területe nagyobb a \(\displaystyle CDM\) háromszög területénél. A négyszög \(\displaystyle BC\) oldalának felezőpontja \(\displaystyle P\), \(\displaystyle CD\) oldalának felezőpontja pedig \(\displaystyle Q\), \(\displaystyle AP+AQ=\sqrt2\,\). Bizonyítsuk be, hogy ekkor az \(\displaystyle ABCD\) négyszög területe kisebb, mint 1.
(5 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. A megoldás során jelölje \(\displaystyle e\) a \(\displaystyle BD\) átló hosszát, \(\displaystyle h_1\), illetve \(\displaystyle h_2\) pedig az \(\displaystyle A\), illetve a \(\displaystyle C\) pont távolságát a \(\displaystyle BD\) átlótól.
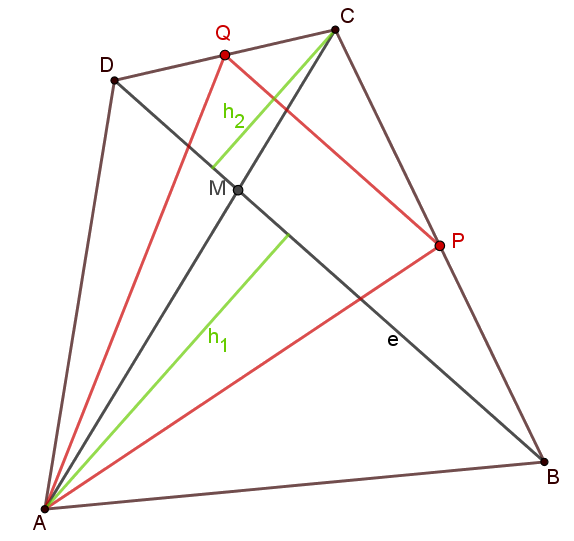
Írjuk fel az \(\displaystyle ABCD\) négyszög területét az \(\displaystyle ABD\) és a \(\displaystyle BCD\) háromszögek területének összegeként:
\(\displaystyle T_{ABCD}=T_{ABD}+T_{BCD}= \frac{e \cdot h_1}{2}+ \frac{e \cdot h_2}{2} = \frac{e \cdot (h_1 + h_2)}{2}.\)
Most nézzük az \(\displaystyle APQ\) háromszög területét, ami kisebb vagy egyenlő, mint \(\displaystyle AP \cdot AQ /2\), hiszen felírható, mint az \(\displaystyle AP\) oldal és a \(\displaystyle Q\) pont \(\displaystyle AP\) oldaltól vett távolságának a szorzatának a fele. Továbbá a számtani és mértani közepek közti összefüggésből \(\displaystyle \sqrt {AP \cdot AQ} \leq \frac{AP+AQ}{2}= \frac{1}{\sqrt2}.\) Ezeket felhasználva kapjuk, hogy
\(\displaystyle T_{APQ} \leq \frac{AP \cdot AQ}{2} \leq \frac14.\)
Másrészt az \(\displaystyle APQ\) háromszög területe felírható a szokásos területképlet segítségével is: \(\displaystyle PQ\) és a hozzá tartozó magasság szorzatának a fele. Mivel \(\displaystyle PQ\) középvonal a \(\displaystyle BCD\) háromszögben, így hossza \(\displaystyle e/2\). A \(\displaystyle PQ\)-hoz tartozó magasság pedig \(\displaystyle h_1+\frac{h_2}{2}\), ismét azt használva, hogy \(\displaystyle PQ\) középvonal a \(\displaystyle BCD\) háromszögben. Tehát:
\(\displaystyle T_{APQ} = \frac{\frac{e}{2} \cdot (h_1 + \frac{h_2}{2})}{2}= \frac{e \cdot (2h_1+h_2)}{8}.\)
Ezeket összevetve adódik, hogy
\(\displaystyle T_{ABCD}=\frac{e(h_1+h_2)}{2} < 4 \cdot \frac{e(2h_1+h_2)}{8}=4 \cdot T_{APQ} \leq 1, \)
ahol az első egyenlőtlenség azért szigorú, mert \(\displaystyle 2h_1\) szerepel \(\displaystyle APQ\) területképletében és nem \(\displaystyle h_1\), és a négyszög konvexitása alapján \(\displaystyle h_1>0\).
Azaz
\(\displaystyle T_{ABCD} < 1.\)
Ezzel megmutattuk, hogy az \(\displaystyle ABCD\) négyszög területe kisebb, mint 1.
Megjegyzés. A feladatban szereplő \(\displaystyle ABM\) és \(\displaystyle CDM\) háromszögek területének nagyságviszonyát nem használtuk a megoldáshoz.
Statisztika:
38 dolgozat érkezett. 5 pontot kapott: Barczikay Ákos, Cserkuti Sándor, Csonka Illés, Feczkó Nóra, Féger Tamás, Fekete András Albert, Hajdú Bálint, Halász Henrik, Horváth Milán, Kalocsai Zoltán, Lőw László, Molnár Réka, Nagy 429 Leila, Németh László Csaba, Németh Máté Előd, Palencsár Enikő, Schneider Anna, Somogyi Dalma, Szalanics Tamás, Viharos Márta Judit. 4 pontot kapott: Andó Lujza, Inokai Dávid. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 5 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2020. áprilisi matematika feladatai

