 |
A C. 1608. feladat (2020. április) |
C. 1608. Jelmezbálra szeretnénk elkészíteni kartonból egy vietnámi kalapot. A kalap egy \(\displaystyle 97{,}18^\circ\) nyílásszögű egyenes körkúp, amelynek alkotója 28 cm hosszú. Elkészíthető-e egy ilyen méretű kalap a kereskedelemben kapható \(\displaystyle 50\times 70\) cm-es kartonpapírból?

(5 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. A kúp alapkörének sugara legyen \(\displaystyle r\), annak középpontja \(\displaystyle O\), a kúp csúcsa \(\displaystyle C\). Vágjuk el a kúpot egy alapkörre merőleges \(\displaystyle O\)-n átmenő síkkal, ekkor síkmetszetként az ábrán látható háromszöget kapjuk.
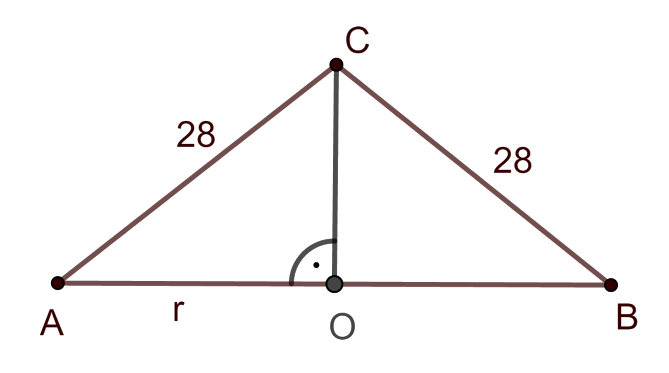
Nézzük az \(\displaystyle AOC\) háromszöget: ez egy derékszögű háromszög, \(\displaystyle C\)-nél levő szögének nagysága a kúp nyílásszögének fele (\(\displaystyle 48,59^{\circ}\)), az \(\displaystyle AC\) átfogó hossza 28 cm. Ebből
\(\displaystyle r=28 \sin 48,59^{\circ} \approx 21.\)
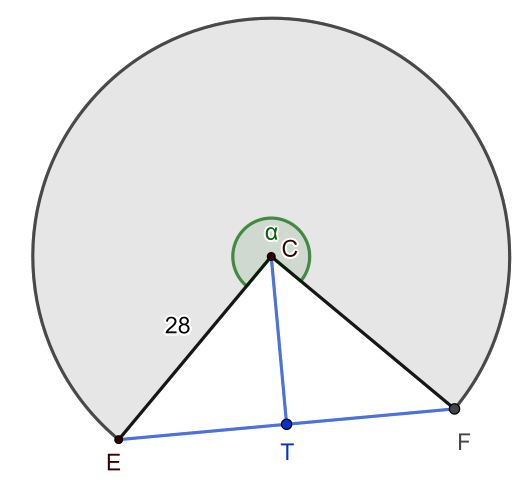
Most nézzük a kalapot kiterítve: Ez egy körcikk, aminek sugara a kúp alkotója, azaz 28 cm. A körív hossza a kúp alapkörének kerületével egyenlő, ami \(\displaystyle 2r\pi \approx 131,95\). A teljes kerülete egy 28 cm sugarú körnek \(\displaystyle 2 \cdot 28 \pi \approx 175,93\), ehhez tartozik a \(\displaystyle 360^{\circ}\)-os középponti szög. A körív hosszának és az imént kiszámolt kerületnek az aránya megadja az \(\displaystyle \alpha\) középponti szög nagyságát:
\(\displaystyle \alpha=\frac{2r\pi}{2 \cdot 28 \pi}\cdot 360^{\circ} \approx 270^{\circ}. \)
Ekkor a kimaradó szög nagysága \(\displaystyle ECF\sphericalangle=360^\circ-\alpha\approx 90^{\circ}\). Vegyük ennek a szögnek a szögfelezőjét, ahol ez metszi \(\displaystyle EF\) szakaszt, az a pont legyen \(\displaystyle T\). \(\displaystyle T\)-nél derékszög van, hiszen a \(\displaystyle CEF\) háromszög egyenlő szárú, ahol a szögfelező magasság is egyben. Ekkor
\(\displaystyle TC= 28\cos(ECT\sphericalangle)=28\cos\left(\frac{ECF\sphericalangle}{2}\right)= 28\cos45^{\circ} \approx 19,8.\)
Tehát a körcikk \(\displaystyle EF\) irányában 56 cm-es (\(\displaystyle EF\) irányában a szélesség épp az átmérő), a rá merőleges irányban pedig
\(\displaystyle 28+CT\approx 47,8\)
cm-es a kiterített kalapunk. Azaz, ha például úgy helyezzük el, hogy \(\displaystyle EF\) illeszkedik a karton egyik 70 cm-es oldalára, és \(\displaystyle T\) az adott oldal felezőpontjába kerül, akkor ráfér, hiszen \(\displaystyle 28+CT<50\). Így elkészíthető a téglalapból a kalap.
Statisztika:
44 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Biró 424 Ádám, Buzás Bence István, Féger Tamás, Fekete András Albert, Hajdú Bálint, Horváth Tamás, Izsa Regina Mária, Kelemen Anna, Kis 194 Károly, Molnár Réka, Pál Mihály, Palencsár Enikő, Pálfi Patrícia, Szabó Csege, Székelyhidi Klára, Szigeti Donát, Tóth Lilla Eszter , Zaránd Andris. 4 pontot kapott: Antal Virág Anna, Arató Zita, Danó Ádám, Kalabay László, Németh Kristóf, Rátki Gergely, Trombitás Karolina Sarolta, Viharos Márta Judit. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 10 versenyző. 1 pontot kapott: 3 versenyző.
A KöMaL 2020. áprilisi matematika feladatai

