 |
A C. 1612. feladat (2020. május) |
C. 1612. Az \(\displaystyle A_1A_2A_3A_4A_5A_6A_7\) konvex hétszög egy olyan körbe írható bele, amelynek középpontja a hétszög belsejében van. Bizonyítsuk be, hogy az \(\displaystyle A_1\), \(\displaystyle A_3\) és \(\displaystyle A_5\) csúcsoknál lévő belső szögek összege kisebb \(\displaystyle 450^{\circ}\)-nál.
(5 pont)
A beküldési határidő 2020. június 10-én LEJÁRT.
Megoldás. Kössük össze a hétszög csúcsait a kör \(\displaystyle O\) középpontjával. Ekkor keletkezik 7 háromszög az ábrán látható módon. Ezen háromszögek mindegyike egyenlő szárú, hisz bármelyik háromszögnek két oldala a körnek sugara.
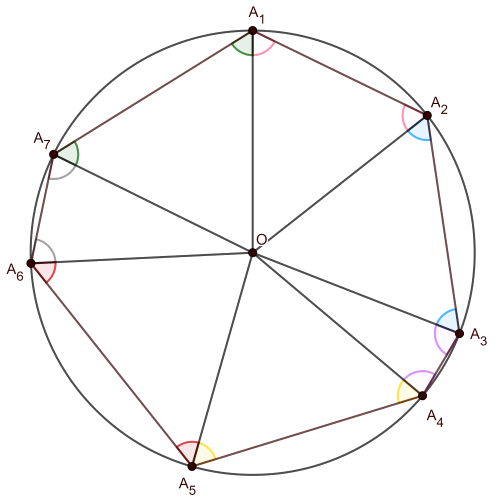
Ezen hét háromszög bármelyikében az alapon fekvő szögek egyenlő nagyságúak. Ezeket az egyenlő szögeket jelöltük azonos színnel az ábrán.
Egy \(\displaystyle n\) oldalú konvex sokszög belső szögeinek összege \(\displaystyle (n-2)\cdot 180^{\circ}\), így a hétszög belső szögeinek összege \(\displaystyle 900^{\circ}\). Ez a \(\displaystyle 900^{\circ}\) nem más, mint a 7 háromszög alapon fekvő szögeinek összege. Tehát ha minden háromszögnek csak egy alapon fekvő szögét tekintjük (minden színes szögből csak egyet veszünk), akkor azok összege \(\displaystyle 450^{\circ}\).
A hétszög \(\displaystyle A_1, A_3\) és \(\displaystyle A_5\) csúcsainál levő belső szögeit tekintve, azokban minden ,,alapon fekvő'' szögből egy szerepel, kivéve az \(\displaystyle A_6A_7O\) háromszögét (egy szín kimarad). Tehát ezen belső szögek összege kisebb, mint \(\displaystyle 450^{\circ}\).
Megjegyzés. Éppen annyival kisebb az összeg \(\displaystyle 450^\circ\)-nál, amekkora az \(\displaystyle A_6A_7O\) szög nagysága. Annál közelebb van az összeg \(\displaystyle 450^\circ\)-hoz, minél közelebb van \(\displaystyle A_6A_7\) hossza a kör átmérőjéhez.
Statisztika:
66 dolgozat érkezett. 5 pontot kapott: 53 versenyző. 4 pontot kapott: 4 versenyző. 3 pontot kapott: 1 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2020. májusi matematika feladatai

