 |
A C. 1624. feladat (2020. október) |
C. 1624. Az \(\displaystyle ABCD\) négyzet \(\displaystyle AB\) oldalának \(\displaystyle P\) pontját kössük össze \(\displaystyle D\)-vel, \(\displaystyle BC\) oldalának \(\displaystyle Q\) pontját pedig \(\displaystyle A\)-val, az így kapott szakaszok metszéspontját jelöljük \(\displaystyle R\)-rel. Az \(\displaystyle ARD\) háromszög területe 1200, az \(\displaystyle APR\) háromszög területe 600, a \(\displaystyle PBQR\) négyszög területe pedig \(\displaystyle 3380-240\sqrt{95}\) egység. Mekkora az \(\displaystyle RQCD\) négyszög területe?
Javasolta: Németh László (Fonyód)
(5 pont)
A beküldési határidő 2020. november 10-én LEJÁRT.
1. megoldás. A megoldáshoz egészítsük ki a feladat elrendezését: az \(\displaystyle AQ\) egyenesének és a \(\displaystyle CD\) oldal egyenesének metszéspontját jelöljük \(\displaystyle E\)-vel, továbbá a \(\displaystyle P\) pontban \(\displaystyle AB\)-re állított merőleges egyenes és \(\displaystyle AQ\) metszéspontja legyen \(\displaystyle F\).
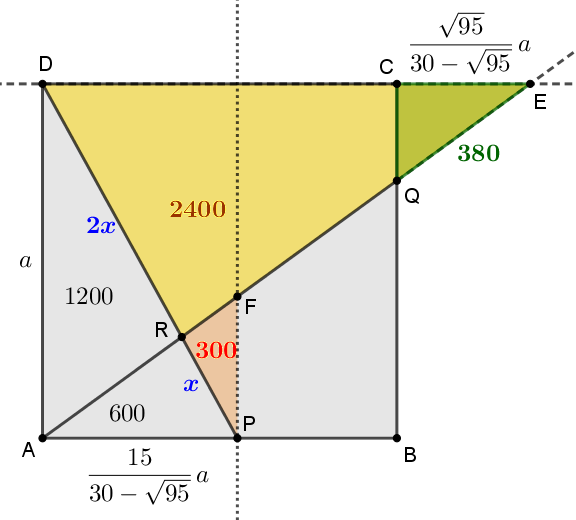
Az \(\displaystyle APR\) és \(\displaystyle ARD\) háromszögek közös \(\displaystyle A\) csúcsából kiinduló magassága megegyezik, mert a két szemközti oldal egy egyenesre esik. A két háromszög területének aránya ezért megegyezik az \(\displaystyle A\)-val szemközti oldalhosszak arányával: \(\displaystyle \displaystyle{\frac{t_{APR}}{t_{ARD}}=\frac{600}{1200}=\frac12=\frac{PR}{RD}}\).
A továbbiakban felhasználjuk azt az összefüggést, hogy ha két hasonló síkidom hasonlóságának aránya \(\displaystyle \lambda\), akkor a területük aránya \(\displaystyle \lambda^2\).
Az \(\displaystyle ARD\triangle\) és \(\displaystyle FRP\triangle\) hasonlóak (mert szögeik páronként megegyeznek: \(\displaystyle R\)-nél csúcsszögek, a másik két szögpár pedig váltószög), a hasonlóság aránya \(\displaystyle \frac12\), ezért \(\displaystyle t_{RPF}=\frac{1200}{4}=300\).
Az \(\displaystyle APF\triangle\) és az \(\displaystyle ABQ\triangle\) is hasonlóak (mert szögeik páronként egyállású szögek, azaz megegyeznek), területük aránya \(\displaystyle \displaystyle{\frac{t_{APF}}{t_{ABQ}}=\frac{900}{600+(3380-240\sqrt{95})}}=\frac{900}{3980-240\sqrt{95}}\). Ekkor a hasonlóság aránya, ami az oldalak aránya, ezen tört négyzetgyöke:
\(\displaystyle \sqrt{\frac{900}{3980-240\sqrt{95}}}=\frac{30}{60-2\sqrt{95}}=\frac{15}{30-\sqrt{95}}.\)
(Abban, hogy a nevező teljes négyzetként felírható, csak reménykedhettünk. Valóban, rövid számolással ellenőrizhető, hogy \(\displaystyle (60-2\sqrt{95})^2=3980-240\sqrt{95}\).)
Ugyanakkor az \(\displaystyle APR\triangle\) hasonló az \(\displaystyle ERD\triangle\)-höz (szögeik páronként megegyeznek: \(\displaystyle R\)-nél csúcsszögek találhatóak, a másik két szögpár pedig váltószög), a hasonlóság aránya \(\displaystyle \frac{PR}{RD}=\frac12\). Így \(\displaystyle ED=2AP\), azaz \(\displaystyle ED\) a négyzet oldalának \(\displaystyle \displaystyle{\frac{30}{30-\sqrt{95}}}\)-szerese; továbbá a háromszögek területének aránya \(\displaystyle \frac14\), azaz \(\displaystyle t_{ERD}=4\cdot 600=2400\).
Végül vizsgáljuk az \(\displaystyle ECQ\triangle\) és \(\displaystyle EDA\triangle\) hasonlóságát (szögek páronként egyállásúak). A \(\displaystyle CE\) szakasz a négyzet oldalához képest annak \(\displaystyle \displaystyle{\frac{30}{30-\sqrt{95}}-1=\frac{\sqrt{95}}{30-\sqrt{95}}}\)-szerese. A két háromszög hasonlóságának aránya ezért \(\displaystyle \frac{EC}{ED}=\frac{\sqrt{95}}{30}\). A területek aránya ennek négyzete: \(\displaystyle \frac{t_{ECQ}}{t_{EDA}}=\frac{t_{ECQ}}{3600}=\frac{95}{900}\), ahonnan \(\displaystyle t_{ECQ}=380\).
Így meghatározható az \(\displaystyle RQCD\) négyszög területe: \(\displaystyle t_{RQCD}=t_{EDR}-t_{ECQ}=2400-380=2020\).
2. megoldás. Vegyünk fel egy koordinátarendszert úgy, hogy
\(\displaystyle A=(0,0),\ B=(a,0),\ C=(a,a),\ D=(0,a)\)
legyen, ahol \(\displaystyle a\) a négyzet oldalának hossza, így a négyzet területe \(\displaystyle t=a^2\). Legyen \(\displaystyle R=(\alpha a,\beta a)\), itt \(\displaystyle 0<\alpha,\beta<1\).
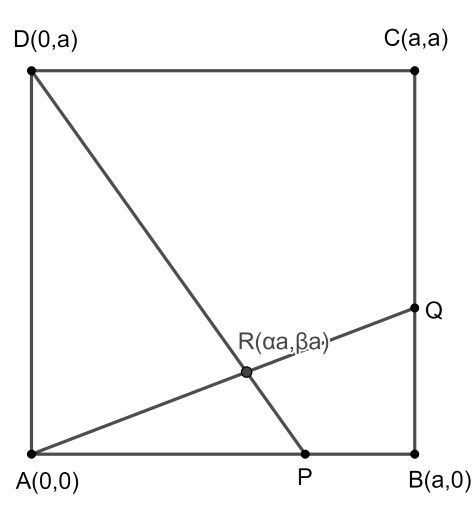
Az \(\displaystyle ARD\) háromszög \(\displaystyle AD\) alapja \(\displaystyle a\) hosszú, ehhez tartozó magassága pedig \(\displaystyle \alpha a\), így
\(\displaystyle t_{ARD}=\frac{\alpha}{2} t.\)
A \(\displaystyle D\) pontból \(\displaystyle \frac{1}{1-\beta}\) arányban kell nagyítanunk, hogy az \(\displaystyle R\) pont képe \(\displaystyle AB\) egyenesére (\(\displaystyle P\)-be) kerüljön, így \(\displaystyle P=(\alpha a/(1-\beta),0)\). Így
\(\displaystyle t_{APD}=\frac{AP\cdot AD}{2}=\frac{\alpha}{2(1-\beta)}t.\)
Az eddigiek alapján
\(\displaystyle 1-\beta=\frac{t_{ARD}}{t_{APD}}=\frac{t_{ARD}}{t_{ARD}+t_{APR}}=\frac{1200}{1200+600}=\frac23,\)
vagyis \(\displaystyle \beta=\frac13\).
Az \(\displaystyle A\) pontból \(\displaystyle \frac{1}{\alpha}\) arányban kell nagyítanunk, hogy \(\displaystyle R\) képe \(\displaystyle BC\)-re (\(\displaystyle Q\)-ba) kerüljön, így \(\displaystyle Q=(a,\beta a/\alpha)\). Ezért
\(\displaystyle t_{ABQ}=\frac{AB\cdot BQ}{2}=\frac{\beta}{2\alpha}t=\frac{1}{6\alpha}t.\)
Mivel \(\displaystyle t_{ARD}=\frac{\alpha}{2} t\) és \(\displaystyle t_{ABQ}=\frac{1}{6\alpha}t\), ezért a két egyenletet összeszorozva \(\displaystyle t\) meghatározható az alábbi számolás szerint:
\(\displaystyle t_{ARD}\cdot t_{ABQ}=\frac{\alpha}{2} t\cdot \frac{1}{6\alpha}t,\)
\(\displaystyle 1200\cdot (600+3380-240\sqrt{95})=\frac{1}{12}t^2,\)
\(\displaystyle \sqrt{12\cdot 1200\cdot (3980-240\sqrt{95})}=t,\)
\(\displaystyle 120\sqrt{3980-240\sqrt{95}}=t,\)
\(\displaystyle 240\sqrt{995-60\sqrt{95}}=t,\)
\(\displaystyle 240(30-\sqrt{95})=t,\)
hiszen a \(\displaystyle 30-\sqrt{95}\) pozitív szám négyzete \(\displaystyle 995-60\sqrt{95}\). Tehát \(\displaystyle t=240(30-\sqrt{95})=7200-240\sqrt{95}\).
A \(\displaystyle t_{ARD}=\frac{\alpha}{2}t\) egyenletből \(\displaystyle \alpha=2t_{ARD}/t=\frac{2400}{7200-240\sqrt{95}}=\frac{10}{30-\sqrt{95}}\approx 0,49\), és könnyen ellenőrizhető, hogy ha a négyzet oldalhosszát \(\displaystyle a=\sqrt{t}=\sqrt{7200-240\sqrt{95}}\)-nek választjuk, \(\displaystyle R\)-et pedig a kapott \(\displaystyle \alpha,\beta\) értékek szerint választjuk meg, akkor teljesülnek a területekre szabott feltételek, \(\displaystyle AB\) és \(\displaystyle DR\) metszéspontja lesz \(\displaystyle P\), \(\displaystyle AR\) és \(\displaystyle BC\) metszéspontja pedig \(\displaystyle Q\). (Ehhez ugyanazokat az egyenleteket kell tekinteni, amelyek segítségével a fentiekben meghatároztuk \(\displaystyle a\), \(\displaystyle \alpha\) és \(\displaystyle \beta\) értékét. Mindez tehát azt jelenti, hogy létezik a feladatban előírt feltételeknek eleget tevő négyzet.)
A feladat az \(\displaystyle RQCD\) négyszög területét kérdezi, ez az eddigiek alapján a következőképpen kapható:
\(\displaystyle t_{RQCD}=t-t_{ARD}-t_{APR}-t_{PBQR}=7200-240\sqrt{95}-1200-600-(3380-240\sqrt{95})=2020.\)
Tehát az \(\displaystyle RQCD\) négyszög területe 2020 egység.
Statisztika:
69 dolgozat érkezett. 5 pontot kapott: Besze Zsolt, Fehérvári Donát, Horváth Milán, Kurucz Kitti, Molnár Kristóf, Nádasdy-Horváth Hunor, Schmercz Blanka, Sipeki Márton, Szabó 423 Ágnes, Szabó Zóra, Werner Kinga, Zádor-Nagy Zsombor. 4 pontot kapott: Csilling Dániel, Deák Gergely, Foris Dávid, Geretovszky Márton László, Győrffy Nándor, Hajós Balázs, Halász Henrik, Hosszu Noel, Josepovits Gábor, Keszthelyi Eszter, Kovács Benedek Noel, Patricia Janecsko, Pekk Márton, Rumpler Bianka, Schleier Anna , Simon 456 Dániel, Szabó Réka, Szamkó Szabolcs, Szirtes Hanna, Vankó Lóránt Albert. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 15 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 2 versenyző. Nem versenyszerű: 5 dolgozat.
A KöMaL 2020. októberi matematika feladatai

