 Problem C. 1631. (November 2020)
Problem C. 1631. (November 2020)
C. 1631. Let \(\displaystyle AB\) be a chord in a unit circle. Triangle \(\displaystyle ABC\) is right-angled at \(\displaystyle B\), and vertex \(\displaystyle C\) lies on the circle. Triangle \(\displaystyle ABD\) is isosceles right-angled, and \(\displaystyle AB\) is the hypotenuse. How long is the chord \(\displaystyle AB\) if the two triangles have equal areas? What is this area?
(5 pont)
Deadline expired on December 10, 2020.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöléseink az ábrán láthatók.
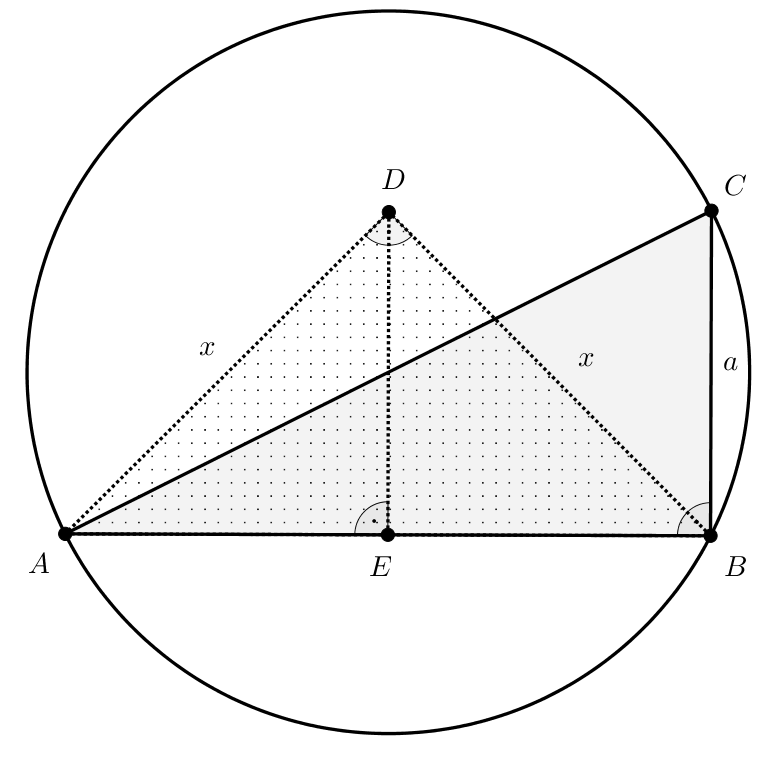
Mivel \(\displaystyle ABC\sphericalangle=90^{\circ}\), ezért \(\displaystyle AC\) az \(\displaystyle ABC\) háromszög körülírt körének átmérője, és így \(\displaystyle AC=2\).
Az \(\displaystyle AD=BD=x\) jelöléssel azt kapjuk, hogy \(\displaystyle AB=x\cdot\sqrt{2}\), és így az ábra \(\displaystyle DE\) szakaszára
\(\displaystyle DE=\frac{x\cdot\sqrt{2}}2\).
A feltétel miatt az \(\displaystyle ABC\) és \(\displaystyle ABD\) háromszögek kétszeres területe is egyenlő, tehát \(\displaystyle a\cdot{AB}=x^2\), azaz \(\displaystyle a\cdot x\cdot \sqrt{2}=x^2\), ahonnan
| \(\displaystyle (1)\) | \(\displaystyle a=\frac{x}{\sqrt{2}}=\frac{x\cdot\sqrt{2}}2.\) |
Felírjuk a Pitagorasz-tételt az \(\displaystyle ABC\) háromszögre:
\(\displaystyle AB^2+BC^2=CA^2\), vagyis \(\displaystyle (x\cdot\sqrt{2})^2+a^2=2^2\). A műveletek elvégzésével és (1) felhasználásával:
| \(\displaystyle (2)\) | \(\displaystyle x=\frac{4}{\sqrt{10}}.\) |
Tudjuk, hogy \(\displaystyle AB=x\cdot\sqrt{2}\), ezért (2) szerint \(\displaystyle AB=\frac{4}{\sqrt{5}}.\)
Az \(\displaystyle ABC\) és \(\displaystyle ABD\) háromszögek területe tehát:
\(\displaystyle T_{ABC}=T_{ABD}=\frac{AB\cdot{a}}2=\frac{x^2}2=0,8.\)
Megjegyzések.
1. A megoldás nyilván nem függ attól, hogy a \(\displaystyle C\) és \(\displaystyle D\) pontokat az \(\displaystyle AB\) egyenes ugyanazon oldalán vettük fel.
2. A megoldásból kiderül, hogy \(\displaystyle BC=DE\), és könnyen bizonyítható, hogy \(\displaystyle CA\) felezi a \(\displaystyle DE\) szakaszt.
Statistics:
164 students sent a solution. 5 points: 72 students. 4 points: 30 students. 3 points: 10 students. 2 points: 11 students. 1 point: 16 students. 0 point: 8 students. Unfair, not evaluated: 17 solutionss.
Problems in Mathematics of KöMaL, November 2020
