Problem C. 1635. (November 2020)

C. 1635. Given two intersecting circles, construct\footnote[1]with straight edge and compasses on paper, or with appropriate geometric construction software a secant through one of the intersection points such that the segment bounded by the two circles is divided \(\displaystyle 1:2\) by the intersection point. Write down and explain the steps of the construction. (Elementary steps like bisecting an angle or reflecting a point in a line do not need to be described in detail.)

(5 pont)

Deadline expired on December 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a két kör \(\displaystyle k\) és \(\displaystyle k'\), a megfelelő középpontok \(\displaystyle O\) és \(\displaystyle O'\), a két kör kiszemelt metszéspontja \(\displaystyle A\).
Az \(\displaystyle A\) ponton áthaladó szelőnek a \(\displaystyle k\) és \(\displaystyle k'\) körökkel való második metszéspontjai legyenek rendre \(\displaystyle B\) és \(\displaystyle C\).
Az \(\displaystyle A\) pont harmadolja a \(\displaystyle BC\) szakaszt, eszerint két lehetőség van: a \(\displaystyle BC\) szakasznak az \(\displaystyle A\) pont
a) a \(\displaystyle B\)-hez közelebb eső harmadolópontja,
b) a \(\displaystyle B\)-től távolabbi harmadolópontja.
Az a) esetben az \(\displaystyle AB\) szakasz hossza fele az \(\displaystyle AC\) szakasz hosszának. Így az \(\displaystyle AC\) felezőpontját \(\displaystyle D_1\)-gyel jelölve \(\displaystyle AB=AD_1=CD_1 \). Az \(\displaystyle O'D_1\) szakasz tehát felezi a \(\displaystyle k'\) kör \(\displaystyle AC\) húrját, de akkor merőleges is rá (1. ábra).

1. ábra

Nyilvánvaló, hogy a \(\displaystyle B\) pontnak az \(\displaystyle A\)-ra vonatkozó tükörképe \(\displaystyle D_1\). Mivel a \(\displaystyle B\) pont nem adott, ezért a \(\displaystyle k\) kört tükrözzük az \(\displaystyle A\)-ra, ekkor kapjuk a \(\displaystyle k_1\) kört. A \(\displaystyle D_1\) pont nem más, mint a \(\displaystyle O'A\) szakasz mint átmérő fölé rajzolt \(\displaystyle d_1\) Thalész-kör és \(\displaystyle k_1\) metszéspontja. A \(\displaystyle D_1\) és \(\displaystyle A\) pontot összekötve megkapjuk a kívánt szelőt.

A szerkesztés módját tekintve teljesen hasonló módon járhatunk el a b) esetben is, de ekkor a \(\displaystyle k'\) körnek az \(\displaystyle A\)-ra vonatkozó tükörképe a \(\displaystyle k_2\) kör, ennek a körnek és az \(\displaystyle AO\) mint átmérő fölé rajzolt \(\displaystyle d_2\) Thalész-körnek a metszéspontja a \(\displaystyle D_2\), és a szerkesztés miatt egyrészt \(\displaystyle D_2\) felezi az \(\displaystyle AB\) szakaszt, másrészt \(\displaystyle AC=AD_2=BD_2\) (2. ábra).

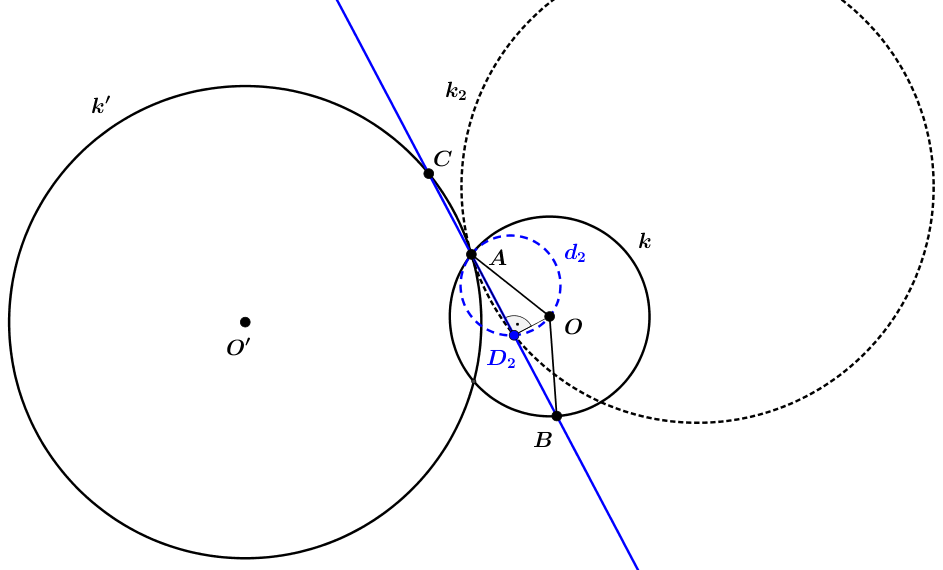
2. ábra

A keresett szelőt az \(\displaystyle AD_2\) egyenesének megrajzolásával szerkeszthetjük meg.
Mind az a), mind a b) esetben egy megoldás van.
Például, mivel a \(\displaystyle d_1\) kör biztosan érinti a \(\displaystyle k'\) kört (az \(\displaystyle A\) pontban), és ha érintené a \(\displaystyle k_1\)-et is, akkor az csak az \(\displaystyle A\) pontban volna lehetséges, de akkor érintenie kellene a \(\displaystyle k_1\)-nek az \(\displaystyle A\)-ra vonatkozó tükörképét, vagyis a \(\displaystyle k\) kört. Ez azonban azt jelentené, hogy \(\displaystyle k\) és \(\displaystyle k'\) is érintik egymást \(\displaystyle A\)-ban, ez viszont ellentmond annak a feltételnek, hogy \(\displaystyle k\) és \(\displaystyle k'\) két pontban metszik egymást. Ezért \(\displaystyle d_1\)-nek és \(\displaystyle k'\)-nek az \(\displaystyle A\) ponton kívül még van egy közös pontja, ez éppen \(\displaystyle D_1\).
Hasonlóan indokolhatjuk, hogy a b) esetben is egy megoldás van.

Megjegyzések.
1. Ha a \(\displaystyle k\) és \(\displaystyle k'\) körök másik metszéspontját is figyelembe vesszük, akkor újabb két megoldást kapunk.
2. Ha a \(\displaystyle k\) és \(\displaystyle k'\) körök az \(\displaystyle A\)-ban érintenék egymást, akkor előfordulhatna, hogy a feladatnak nincs megoldása, de az is, hogy végtelen sok megoldása van. Utóbbi éppen akkor következne be, ha a két kör sugarának aránya \(\displaystyle 1:2\) lenne.

Statistics:

20 students sent a solution.
5 points:	Biró 424 Ádám, Dobi Dorina Lili, Egyházi Hanna, Féger Tamás, Fonyi Máté Sándor, Kadem Aziz, Molnár Réka, Schneider Anna.
4 points:	Andó Lujza, Fekete András Albert, Szalanics Tamás, Téglás Panna.
3 points:	3 students.
2 points:	2 students.
1 point:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, November 2020