A C. 1637. feladat (2020. december)

C. 1637. Sárkányországban minden hétfejű sárkány tüzet okád, de nem minden hétfejű tűzokádó lény sárkány. A legutóbbi lényszámlálás szerint az országban pont ugyanannyi sárkány él, mint tűzokádó lény. Igaz-e, hogy minden sárkány hétfejű?

(5 pont)

A beküldési határidő 2021. január 11-én LEJÁRT.

Megoldás. Megmutatjuk, hogy nem igaz.

Ha minden sárkány hétfejű lenne, akkor az első feltétel alapján az is teljesülne, hogy mind tüzet okádnak. Azaz minden sárkány tűzokádó lenne. Mivel ugyanannyi sárkány van, mint tűzokádó lény, ezért ez azt jelentené, hogy mindez megfordítva is igaz: minden tűzokádó lény sárkány. Ez azonban ellentmond annak, hogy nem minden hétfejű tűzokádó lény sárkány, ez a feltétel ugyanis azt jelenti, hogy van olyan tűzokádó lény, aminek egyrészt hét feje van (de ez most nem játszik szerepet), másrészt nem sárkány.

Megjegyzés. Az ilyen típusú feladatoknál érdemes Venn-diagramot készíteni (lásd az alábbi ábrát, ahol \(\displaystyle S\) a sárkányok, \(\displaystyle H\) a hétfejűek, \(\displaystyle T\) pedig a tűzokádó lények halmaza).

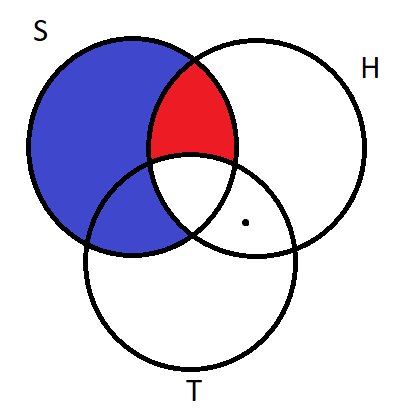
Az a feltétel, hogy minden hétfejű sárkány tüzet okád, azt jelenti, hogy a pirossal jelölt rész (\(\displaystyle S\cap H \setminus T\)) üres. Az pedig, hogy nem minden hétfejű tüzet okádó lény sárkány azt jelenti, hogy \(\displaystyle H\cap T\setminus S\ne \emptyset\) (az ábrán egy pont jelöli, hogy ebben a részben legalább egy elem található). Ha minden sárkány hétfejű lenne, az azt jelentené, hogy \(\displaystyle S\setminus H\) (az ábrán kékkel jelölt rész) üres. Ekkor viszont az összes sárkány \(\displaystyle S\cap H\cap T\) eleme lenne, így mivel \(\displaystyle H\cap T\setminus S\)-ben is van legalább egy lény, több tűzokádó lenne, mint sárkány, ellentétben a megadott feltétellel.

Statisztika:

181 dolgozat érkezett.
5 pontot kapott:	167 versenyző.
0 pontot kapott:	6 versenyző.
Nem versenyszerű:	7 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2020. decemberi matematika feladatai