Problem C. 1640. (December 2020)

C. 1640. In a quadrilateral \(\displaystyle ABCD\), let \(\displaystyle S\) denote the centroid of triangle \(\displaystyle ABC\), and let \(\displaystyle P\) denote the centroid of triangle \(\displaystyle ACD\). Prove that the line segment connecting the midpoints of diagonals \(\displaystyle AC\) and \(\displaystyle BD\) bisects the line segment \(\displaystyle SP\).

(5 pont)

Deadline expired on January 11, 2021.

Sorry, the solution is available only in Hungarian. Google translation

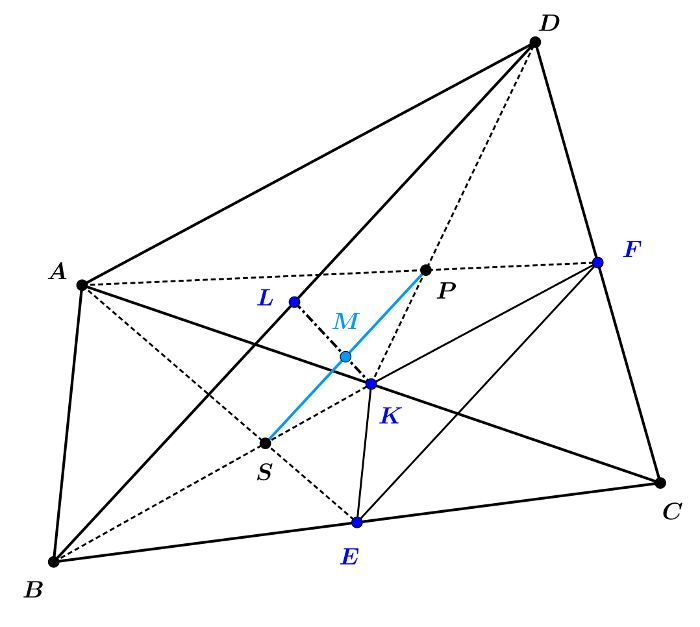
Megoldás. Legyen először \(\displaystyle ABCD\) konvex négyszög, amelyben a \(\displaystyle BC\) és \(\displaystyle CD\) oldalak felezőpontja rendre \(\displaystyle E\) és \(\displaystyle F\), az \(\displaystyle AC\) és \(\displaystyle BD\) átlók felezőpontja rendre \(\displaystyle K\) és \(\displaystyle L\), legyen továbbá a \(\displaystyle KL\) és \(\displaystyle SP\) szakaszok metszéspontja \(\displaystyle M\). Megmutatjuk, hogy \(\displaystyle M\) az \(\displaystyle SP\) szakasz felezőpontja (1. ábra).

1. ábra

Mivel \(\displaystyle S\) az \(\displaystyle ABC\) háromszög súlypontja, ezért a súlypont tulajdonsága alapján \(\displaystyle \frac{KS}{KB}=\frac{1}{3}\).

A \(\displaystyle P\) pont pedig az \(\displaystyle ACD\) háromszög súlypontja, ezért \(\displaystyle \frac{KP}{KD}=\frac{1}{3}\).

A \(\displaystyle BKD\sphericalangle\) szárait tehát úgy metszettük el az \(\displaystyle SP\) és \(\displaystyle BD\) szakaszokkal, hogy

\(\displaystyle \frac{KS}{KB}=\frac{KP}{KD}=\frac{1}{3}\).

A párhuzamos szelők tételének megfordítása szerint ez azt jelenti, hogy \(\displaystyle SP\) párhuzamos \(\displaystyle BD\)-vel, tehát az \(\displaystyle SPDB\) négyszög trapéz, amelynek \(\displaystyle BS\) és \(\displaystyle DP\) szárai a \(\displaystyle K\) pontban metszik egymást.

Alkalmazhatjuk tehát a párhuzamos szelőszakaszok tételét az \(\displaystyle SM\) szakasz hosszának kifejezésére: \(\displaystyle \frac{SM}{BL}=\frac{KS}{KB}=\frac{1}{3}\), ahonnan \(\displaystyle SM=\frac{BL}{3}\).

Hasonlóképpen számíthatjuk ki a \(\displaystyle PM\) szakasz hosszát is: \(\displaystyle \frac{PM}{DL}=\frac{KP}{KD}=\frac{1}{3}\), ezért \(\displaystyle PM=\frac{DL}{3}\).

Tudjuk, hogy \(\displaystyle L\) felezi a \(\displaystyle BD\) szakaszt, vagyis \(\displaystyle BL=DL\), így az előző összefüggésekből \(\displaystyle SM=PM\) következik, \(\displaystyle M\) tehát valóban felezőpontja az \(\displaystyle SP\) szakasznak.

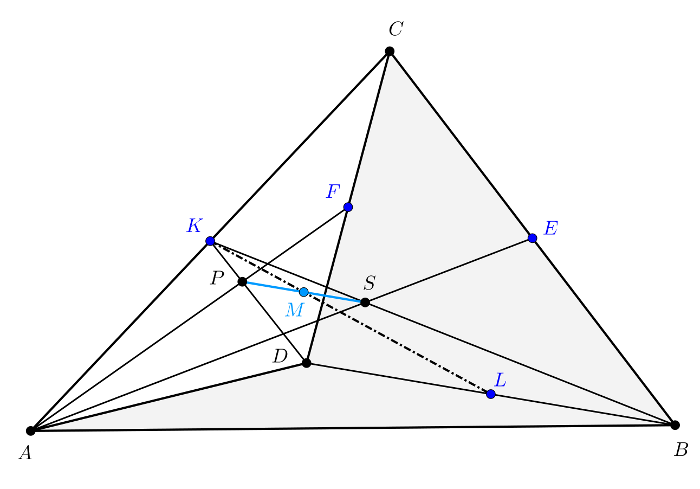
Hasonló módon igazolható a feladat állítása konkáv négyszögre is. Legyen például az \(\displaystyle ABCD\) konkáv négyszögben a \(\displaystyle D\) csúcshoz tartozó belső szög homorúszög. Tekintsük az ennek megfelelő 2. ábrát.

2. ábra

Felírt összefüggéseink és megállapításaink pontról pontra megegyeznek a konvex négyszög esetén leírtakkal, ezért ismét azt kapjuk, hogy \(\displaystyle KL\) és \(\displaystyle SP\) \(\displaystyle M\) metszéspontja az \(\displaystyle SP\) szakasz felezőpontja.

Megjegyzések.

1. Bizonyításunkból az is látszik, hogy az \(\displaystyle M\) pont mindig létrejön mint az \(\displaystyle SP\) és \(\displaystyle KL\) szakaszok közös pontja, hiszen \(\displaystyle SP\) párhuzamos \(\displaystyle BD\)-vel és az \(\displaystyle SPDB\) trapéz szárainak \(\displaystyle K\) metszéspontját a \(\displaystyle BD\) alap \(\displaystyle L\) felezőpontjával összekötő szakasz felezi a trapéz \(\displaystyle SP\) alapját is. Előfordulhat azonban, hogy a \(\displaystyle K\) és \(\displaystyle L\) pontok egybeesnek. Ez esetben az \(\displaystyle ABCD\) négyszög nyilvánvalóan paralelogramma, amelyben az \(\displaystyle SP\) szakasz felezőpontja és a \(\displaystyle K=L\) pont azonos. A feladat állítása ekkor is teljesül, noha a \(\displaystyle KL\) szakasz egy ponttá zsugorodik.

2. A konkáv négyszögre elmondottak érvényesek akkor is, ha a négyszögben valamelyik másik csúcshoz tartozó belső szög homorú.

3. Az állítás akkor is könnyen igazolható, ha a feladatbeli \(\displaystyle ABC\) és \(\displaystyle ACD\) háromszögek létrejönnek, de az \(\displaystyle ABCD\) négyszögnek három csúcsa egy egyenesre esik, vagyis egyik belső szöge \(\displaystyle 180^{\circ}\)-os. Ez valósul meg például akkor, ha a \(\displaystyle C\) pont a \(\displaystyle BD\) szakasz belső pontja.

Statistics:

131 students sent a solution.
5 points:	109 students.
4 points:	2 students.
3 points:	8 students.
2 points:	2 students.
0 point:	8 students.
Unfair, not evaluated:	1 solutions.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, December 2020