 Problem C. 1645. (January 2021)
Problem C. 1645. (January 2021)
C. 1645. In an acute-angled triangle, the sides are \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), and \(\displaystyle m_b\) is the height drawn to side \(\displaystyle b\). The lengths of \(\displaystyle m_b\), \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), in this order, are consecutive positive integers. What is the area of the triangle?
Proposed by Zs. M. Tatár, Esztergom
(5 pont)
Deadline expired on February 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az \(\displaystyle ABC\) háromszög hegyesszögű, ezért minden magassága a háromszögön belül van, így az \(\displaystyle m_b\) magasság is, az \(\displaystyle m_b\) magasság \(\displaystyle D\) talppontja pedig a \(\displaystyle CA\) oldal belső pontja. Tekintsük a következő ábrát.
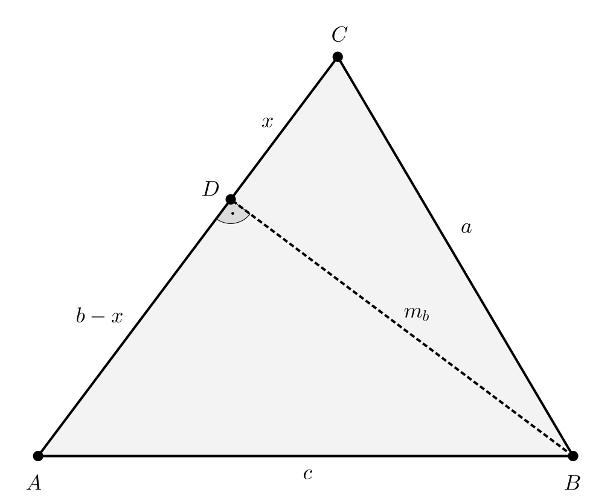
A feltétel szerint az \(\displaystyle m_b\), \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) ebben a sorrendben egymás utáni pozitív egész számok, ezért \(\displaystyle m_b=a-1\), \(\displaystyle b=a+1\) és \(\displaystyle c=a+2\).
Az ábra \(\displaystyle ABD\) és \(\displaystyle BCD\) derékszögű háromszögeire felírt Pitagorasz-tételekből azt kapjuk, hogy \(\displaystyle c^2-(b-x)^2=a^2-x^2\), azaz
\(\displaystyle (a+2)^2-((a+1)-x)^2=a^2-x^2.\)
Végezzzük el a műveleteket és rendezzük az egyenletet:
\(\displaystyle a^2+4a+4-(a^2+2a+1-2ax-2x+x^2)=a^2-x^2,\)
\(\displaystyle a^2-2a-3=2(a+1)x.\)
Az egyenlet bal oldala szorzattá alakítható:
\(\displaystyle (a+1)(a-3)=2(a+1)x,\)
amelyből a nyilván pozitív \(\displaystyle a+1\) tényezővel osztva azt kapjuk, hogy
| \(\displaystyle (1)\) | \(\displaystyle x=\frac{a-3}{2}.\) |
Az ábra \(\displaystyle BCD\) háromszögére felírhatjuk a Pitagorasz-tételt: \(\displaystyle x^2+(a-1)^2=a^2\), vagyis (1) alapján
\(\displaystyle \frac{(a-3)^2}{4}+(a-1)^2=a^2.\)
Végezzük el a műveleteket és rendezzük az egyenletet:
\(\displaystyle a^2-6a+9+(4a^2-8a+4)=4a^2,\)
| \(\displaystyle (2)\) | \(\displaystyle a^2-14a+13=0.\) |
A (2) másodfokú egyenlet gyökei: \(\displaystyle a_1=1\) és \(\displaystyle a_2=13\).
Az \(\displaystyle a_1=1\) nyilván nem megoldás, mert ebben az esetben az \(\displaystyle m_b\) magasság hossza \(\displaystyle 0\) lenne. Ezért csak az \(\displaystyle a_2=13\) megoldása a feladatnak. Ezt figyelembe véve \(\displaystyle m_b=12, a=13, b=14\) és \(\displaystyle c=15\).
A háromszög területe tehát (területegységben számolva):
\(\displaystyle T=\frac{b\cdot{m_b}}{2}=\frac{14\cdot12}{2}=84.\)
Statistics:
116 students sent a solution. 5 points: 63 students. 4 points: 26 students. 3 points: 8 students. 2 points: 7 students. 1 point: 7 students. 0 point: 4 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, January 2021
