 Problem C. 1647. (January 2021)
Problem C. 1647. (January 2021)
C. 1647. The medians drawn to the legs of an isosceles triangle are perpendicular to each other. Let \(\displaystyle r\) and \(\displaystyle R\) denote the inradius and circumradius, respectively. Find the exact value of the ratio \(\displaystyle \frac{r}{R}\).
(5 pont)
Deadline expired on February 15, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöléseink az ábrán láthatók, ahol az \(\displaystyle BC\) és \(\displaystyle AC\) szárak felezőpontjait rendre \(\displaystyle D, E\)-vel, az \(\displaystyle AB\) alap felezőpontját \(\displaystyle F\)-fel jelöltük.
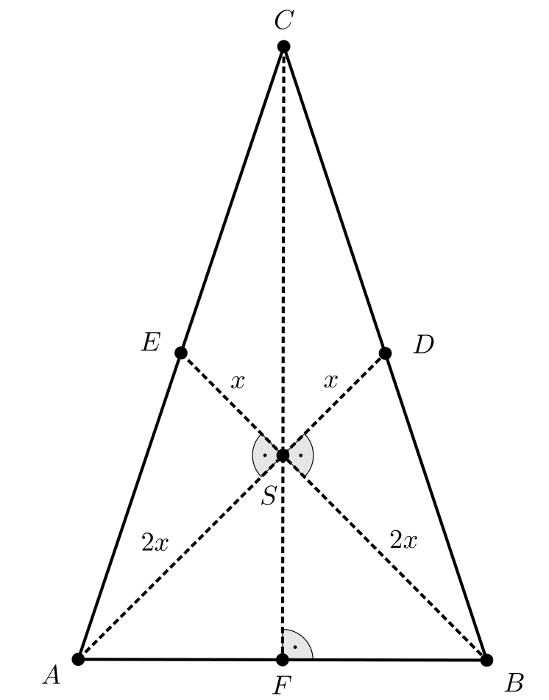
Az egyenlő szárú háromszög az \(\displaystyle AB\) alap \(\displaystyle CF\) felezőmerőlegesére szimmetrikus, ezért ha \(\displaystyle SD=x\), akkor \(\displaystyle SE=x\) is igaz, a súlypont pedig a súlyvonalak csúcstól távolabb eső harmadolópontja, tehát \(\displaystyle SA=SB=2x\).
A feltétel alapján az \(\displaystyle ABS\) háromszög egyenlő szárú, derékszögű háromszög, ezért
| \(\displaystyle (1)\) | \(\displaystyle AB=2x\cdot{\sqrt{2}}.\) |
Az \(\displaystyle ASE\) és \(\displaystyle BSD\) egybevágó derékszögű háromszögek, ezért a Pitagorasz-tétel alkalmazása után azt kapjuk, hogy
\(\displaystyle \frac{AC}{2}=\frac{BC}{2}=AE=BD=x\cdot{\sqrt{5}},\)
így
| \(\displaystyle (2)\) | \(\displaystyle AC=BC=2x\cdot{\sqrt{5}}.\) |
Ebből (1) és (2) alapján az következik, hogy az \(\displaystyle ABC\) háromszög kerülete:
| \(\displaystyle (3)\) | \(\displaystyle K_{ABC}=2x\cdot({\sqrt{2}+2{\sqrt{5}}}).\) |
Bármely háromszög súlyvonala felezi a háromszög területét, ezért az \(\displaystyle ABC\) háromszög területe:
| \(\displaystyle (4)\) | \(\displaystyle T_{ABC}=2\cdot{T_{ABD}}=2\cdot{\frac{3x\cdot{2x}}{2}}=6x^2.\) |
Ismeretes, hogy minden háromszögben \(\displaystyle \frac{T}{K}=\frac{r}{2}\), ezért (3) és (4) felhasználásával
\(\displaystyle r=\frac{2\cdot{T_{ABC}}}{K_{ABC}}=\frac{12x^2}{2x\cdot({\sqrt{2}+2{\sqrt{5}}})}.\)
A törtet egyszerűsítve és a nevezőt gyöktelenítve:
| \(\displaystyle (5)\) | \(\displaystyle r=x\cdot{\frac{6(2\sqrt{5}-\sqrt{2})}{20-2}}=x\cdot{\frac{2\sqrt{5}-\sqrt{2}}{3}}.\) |
Minden háromszögben érvényes az
\(\displaystyle R=\frac{abc}{4T}\)
összefüggés, ezért
\(\displaystyle R=\frac{2x\cdot\sqrt{5}\cdot2x\cdot\sqrt{5}\cdot2x\cdot\sqrt{2}}{24x^2},\)
ebből egyszerűsítés után adódik, hogy:
| \(\displaystyle (6)\) | \(\displaystyle R=x\cdot{\frac{5\sqrt{2}}{3}}.\) |
Az (5) és (6) eredmények felhasználásával a beírt és körülírt kör sugarának aránya:
\(\displaystyle \frac{r}{R}=x\cdot{\frac{2\sqrt{5}-\sqrt{2}}{3}}\cdot\frac{3}{x\cdot5\sqrt{2}}.\)
Egyszerűsítve és a nevezőt négyzetgyöktelenítve:
\(\displaystyle \frac{r}{R}=\frac{2\sqrt5-\sqrt2}{5\sqrt2}=\frac{2\sqrt{10}-2}{10}=\frac{\sqrt{10}-1}{5},\)
ez a feltételeknek megfelelő egyenlőszárú háromszög beírt és körülírt körei sugarának arányára adott pontos érték.
Statistics:
122 students sent a solution. 5 points: 80 students. 4 points: 28 students. 3 points: 4 students. 2 points: 1 student. 1 point: 3 students. 0 point: 5 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, January 2021
