 |
A C. 1652. feladat (2021. február) |
C. 1652. Két derékszögű háromszögnek egységnyi a rövidebb befogója. Mindkettő háromszögben a derékszögnél levő csúcs egységnyire van az átfogó harmadolópontjától: az egyik esetében a közelebbi, a másik esetében a távolabbi harmadolóponttól. Igazoljuk, hogy a háromszögek egységtől különböző oldalai között van három, amelyből derékszögű háromszög szerkeszthető.
(5 pont)
A beküldési határidő 2021. március 10-én LEJÁRT.
1. megoldás. Tekintsük a következő ábrát, amelyen a feladatban szereplő mindkét háromszöget ábrázoltuk.
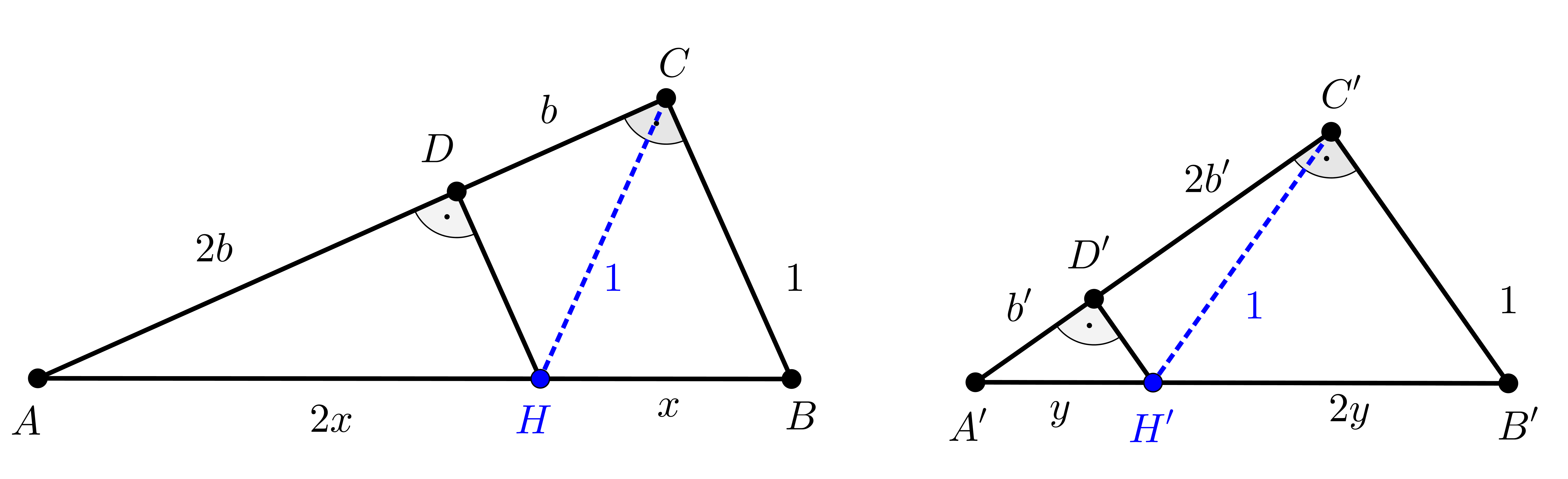
A feltételeknek megfelelően az \(\displaystyle ABC\) háromszögben az \(\displaystyle AB\) átfogó \(\displaystyle B\)-hez közelebbi harmadolópontja \(\displaystyle H\), míg az \(\displaystyle A'B'C'\) háromszögben az \(\displaystyle A'B'\) átfogó \(\displaystyle A'\)-höz közelebbi harmadolópontja \(\displaystyle H'\).
A \(\displaystyle H\), illetve \(\displaystyle H'\) pontból merőlegest állítottunk az \(\displaystyle AC\), illetve \(\displaystyle A'C'\) befogókra, így kaptuk az egyik háromszögben a \(\displaystyle D\), a másikban a \(\displaystyle D'\) pontot.
Nyilvánvaló, hogy \(\displaystyle BC\parallel{HD}\) és \(\displaystyle B'C'\parallel{H'D'}\), ezért alkalmazhatjuk a párhuzamos szelők, illetve szelőszakaszok tételét. Ennek megfelelően az \(\displaystyle ABC\) háromszögben a \(\displaystyle BH=x\) és \(\displaystyle CD=b\) jelöléssel azt kapjuk, hogy:
\(\displaystyle AH=2x;\qquad{AD=2b},\)
valamint
\(\displaystyle HD=\frac{2}{3}.\)
Hasonlóképpen kapjuk az \(\displaystyle A'B'C'\) háromszögből az \(\displaystyle A'H'=y\) és \(\displaystyle A'D'=b'\) jelöléssel:
\(\displaystyle B'H'=2y;\qquad{C'D'=2b'},\)
illetve
\(\displaystyle H'D'=\frac{1}{3}.\)
A \(\displaystyle HCD\) és \(\displaystyle H'C'D'\) derékszögű háromszögekben felírjuk a Pitagorasz-tételt:
| \(\displaystyle (1)\) | \(\displaystyle b^2+\Bigg(\frac{2}{3}\Bigg)^2=1,\) |
valamint
| \(\displaystyle (2)\) | \(\displaystyle (2b')^2+\Bigg(\frac{1}{3}\Bigg)^2=1.\) |
Az (1) és (2) egyenletek megoldásával:
\(\displaystyle b=\frac{\sqrt{5}}{3}; \qquad{b'=\frac{\sqrt{2}}{3}}.\)
Ebből az következik, hogy az \(\displaystyle ABC\) háromszögben \(\displaystyle AC=3b=\sqrt{5}\), és így a Pitagorasz-tételből adódóan \(\displaystyle AB=\sqrt{6}\). Hasonlóan egyszerűen kapjuk, hogy az \(\displaystyle A'B'C'\) háromszögben \(\displaystyle A'C'=3b'=\sqrt{2}\), és így a Pitagorasz-tétel felhasználásával \(\displaystyle A'B'=\sqrt{3}\). A feladat feltételeinek megfelelő két derékszögű háromszög egységtől különböző oldalai tehát:
\(\displaystyle AB=\sqrt{6},\quad AC=\sqrt{5};\qquad{A'B'=\sqrt{3},\quad A'C'=\sqrt{2}}.\)
A Pitagorasz-tétel megfordítása alapján könnyen látható, hogy az \(\displaystyle AC, A'B', A'C'\) szakaszokból derékszögű háromszög szerkeszthető (éspedig a négy szakasz közül csak ebből a háromból), hiszen
\(\displaystyle \big(\sqrt{5}\big)^2=\big(\sqrt{3}\big)^2+\big(\sqrt{2}\big)^2.\)
Ezzel a megoldást befejeztük.
2. megoldás. Illesszük össze a két derékszögű háromszöget úgy, hogy az egységnyi befogójuk azonos legyen, ezzel a másik két befogó egyenese is ugyanaz az egyenes lesz. Tekintsük a következő ábrát, amelyen a \(\displaystyle C\) pontból az \(\displaystyle A, B, D, E, F\) pontokba rendre az \(\displaystyle \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{d}, \overrightarrow{e}, \overrightarrow{f}\) vektorokat indítottuk, ahol az \(\displaystyle AB\) átfogó \(\displaystyle A\)-hoz közelebbi harmadolópontja \(\displaystyle E\) és a másik háromszög \(\displaystyle AD\) átfogójának \(\displaystyle A\)-tól távolabbi harmadolópontja \(\displaystyle F\).
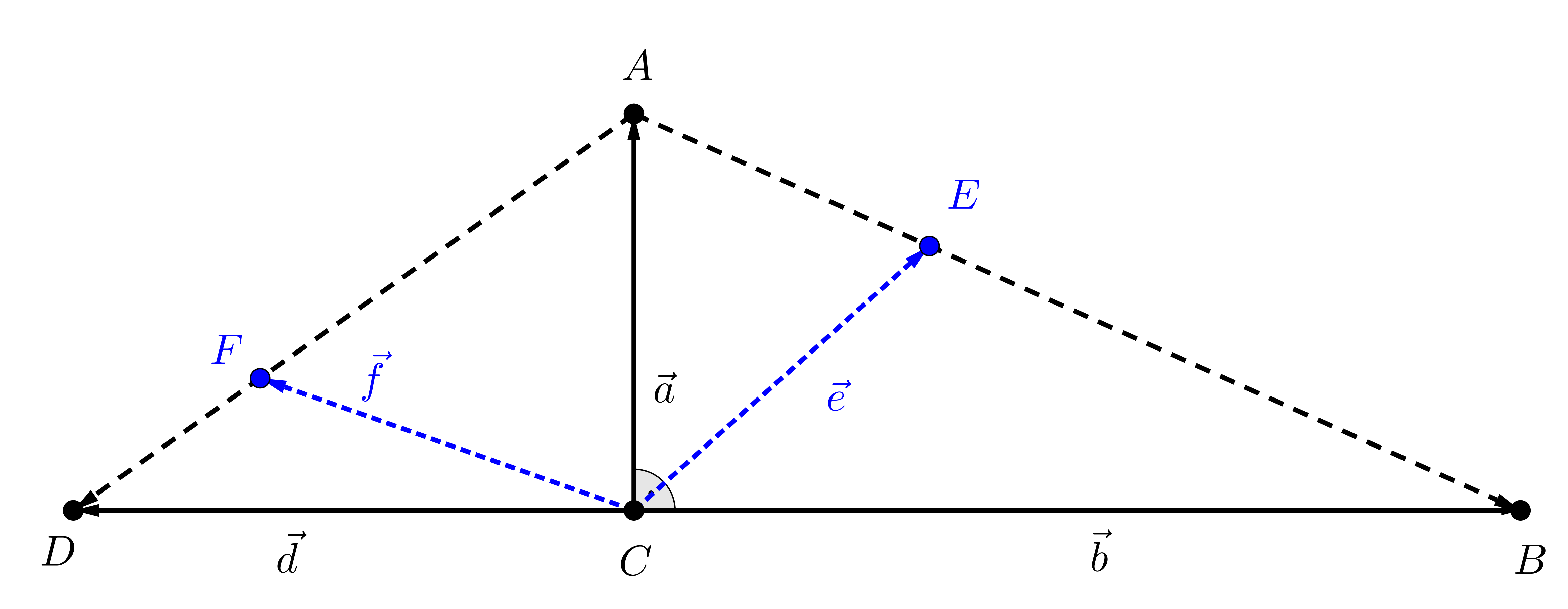
Az \(\displaystyle \overrightarrow{a}, \overrightarrow{e}, \overrightarrow{f}\) vektorok hossza a feltételek szerint egységnyi, azaz \(\displaystyle |\overrightarrow{a}|=|\overrightarrow{e}|=|\overrightarrow{f}|=1.\) A továbbiakban a \(\displaystyle \overrightarrow{b}\) és \(\displaystyle \overrightarrow{d}\) vektorok hosszának megállapítására törekszünk. Az \(\displaystyle \overrightarrow{AB}\) és az \(\displaystyle \overrightarrow{AD}\) vektorok előállíthatók az \(\displaystyle \overrightarrow{a}, \overrightarrow{b}, \overrightarrow{d}\) vektorok segítségével a következőképpen:
| \(\displaystyle (1)\) | \(\displaystyle \overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a};\qquad{\overrightarrow{AD}=\overrightarrow{d}-\overrightarrow{a}}.\) |
Az \(\displaystyle E\) és \(\displaystyle F\) pontok rendre az \(\displaystyle AB\) és \(\displaystyle AD\) oldalak \(\displaystyle A\)-hoz közelebbi, illetve távolabbi harmadolópontjai, ezért (1) szerint:
| \(\displaystyle (2)\) | \(\displaystyle \overrightarrow{AE}=\frac{1}{3}\cdot(\overrightarrow{b}-\overrightarrow{a});\qquad{\overrightarrow{AF}=\frac{2}{3}\cdot(\overrightarrow{d}-\overrightarrow{a})}.\) |
Ugyanakkor \(\displaystyle \overrightarrow{e}=\overrightarrow{a}+\overrightarrow{AE}\) és \(\displaystyle \overrightarrow{f}=\overrightarrow{a}+\overrightarrow{AF}\), ebből (2) felhasználásával azt kapjuk, hogy
| \(\displaystyle (3)\) | \(\displaystyle \overrightarrow{e}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b};\qquad{\overrightarrow{f}=\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{d}}.\) |
Ismeretes, hogy az \(\displaystyle \overrightarrow{u}\) és \(\displaystyle \overrightarrow{v}\) vektorok skaláris szorzata
\(\displaystyle \overrightarrow{u}\cdot\overrightarrow{v}=|\overrightarrow{u}|\cdot|\overrightarrow{v}|\cdot\cos{\varphi},\)
ahol \(\displaystyle \varphi\) a két vektor iránya által bezárt szög. Képezzük a (3) alatti vektorok önmagukkal való skaláris szorzatát. Mivel egy vektor önmagával \(\displaystyle 0^{\circ}\)-os szöget zár be, és így \(\displaystyle \cos{\varphi}=1\), ezért ezek a skaláris szorzatok a vektorok hosszának négyzetét fogják adni, vagyis mind az \(\displaystyle \overrightarrow{e}\), mind az \(\displaystyle \overrightarrow{f}\) esetén \(\displaystyle 1\)-et. Felhasználjuk még azt, hogy az \(\displaystyle \overrightarrow{a}\) és \(\displaystyle \overrightarrow{b}\), illetve \(\displaystyle \overrightarrow{a}\) és \(\displaystyle \overrightarrow{d}\) vektorok skaláris szorzata zérus, hiszen ezek a vektorpárok merőlegesek egymásra és így \(\displaystyle \cos{\varphi}=0\).
Ebből következően:
| \(\displaystyle (4)\) | \(\displaystyle \frac{4}{9}+\frac{1}{9}b^2=1;\qquad{\frac{1}{9}+\frac{4}{9}d^2}=1,\) |
ahol \(\displaystyle |\overrightarrow{b}|=b\) és \(\displaystyle |\overrightarrow{d}|=d\). A (4) egyenletek megoldásával azt kapjuk, hogy
\(\displaystyle b=\sqrt{5};\qquad{d=\sqrt{2}}.\)
A Pitagorasz-tétel alkalmazásával megkapjuk az ábra háromszögeinek hiányzó oldalait, és ezzel a feladat feltételeinek megfelelő derékszögű háromszögek egységtől különböző oldalai:
\(\displaystyle AB=\sqrt{6},\quad CB=\sqrt{5};\qquad{AD=\sqrt{3},\quad CD=\sqrt{2}}.\)
A Pitagorasz-tétel megfordítása szerint az \(\displaystyle CB, AD, CD\) szakaszokból derékszögű háromszög szerkeszthető (a négy szakasz közül csak ebből a háromból), mivel
\(\displaystyle \big(\sqrt{5}\big)^2=\big(\sqrt{3}\big)^2+\big(\sqrt{2}\big)^2.\)
Ezzel a megoldást befejeztük.
Statisztika:
81 dolgozat érkezett. 5 pontot kapott: Fehérvári Donát, Fekete Patrik, Gecseg Bence, Horváth 530 Mihály, Hosszu Noel, Jójárt Emese, Keszthelyi Eszter, Murai Dóra Eszter, Nagy Flóra, Pekk Márton, Radzik Réka, Simon 456 Dániel, Szabó Zóra, Waldhauser Miklós, Wrana Gergő. 4 pontot kapott: 44 versenyző. 3 pontot kapott: 14 versenyző. 2 pontot kapott: 7 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2021. februári matematika feladatai

