 Problem C. 1653. (February 2021)
Problem C. 1653. (February 2021)
C. 1653. How many solutions does the inequality
\(\displaystyle |x|+|y|<2021 \)
have over the set of pairs of integers?
(5 pont)
Deadline expired on March 10, 2021.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Mivel egész megoldásokat keresünk, a feladat ekvivalens az
\(\displaystyle |x|+|y|\leq2020\)
egyenlőtlenséggel.
Számoljuk össze először, hogy hány megoldás van \(\displaystyle x,y>0\) esetén. Ha \(\displaystyle x=2020\), akkor \(\displaystyle y\) értéke csak \(\displaystyle 0\) lehetne.
Ha \(\displaystyle x=2019\), akkor \(\displaystyle y\) értéke csak \(\displaystyle 1\) lehet, ez 1 eset.
Ha \(\displaystyle x=2018\), akkor \(\displaystyle y\) értéke \(\displaystyle 1\) vagy \(\displaystyle 2\) lehet, ez 2 eset.
És így tovább, \(\displaystyle x\) értékét mindig 1-gyel csökkentve \(\displaystyle y\) eggyel többféle értéket vehet fel. Ha \(\displaystyle x=1\), akkor \(\displaystyle y\) értéke lehet \(\displaystyle 1\), \(\displaystyle 2\), ..., \(\displaystyle 2019\).
Ez összesen
\(\displaystyle 1+2+3...+2019=\frac{(1+2019)\cdot2019}{2}=\frac{2020\cdot2019}{2}=2\,039\,190\)
lehetőség.
Minden egyes \(\displaystyle (a;b)\) számpárhoz, ahol \(\displaystyle a,b>0\) tartozik három másik megfelelő számpár: \(\displaystyle (-a;b)\), \(\displaystyle (a;-b)\) és \(\displaystyle (b;-a)\), tehát az előbb kapott esetek négyszerese azon számpárok halmaza, ahol egyik szám sem 0.
Ha \(\displaystyle x=0\), akkor \(\displaystyle y\) értéke \(\displaystyle -2020\) és \(\displaystyle 2020\) között bármilyen egész szám lehet, ez 4041 eset. Ha \(\displaystyle y=0\), az ugyanígy 4041 eset, de a \(\displaystyle (0;0)\) esetet mindkettőbe beleszámoltuk.
Tehát a kérdéses számpárok száma összesen:
\(\displaystyle 4\cdot2\,039\,190+2\cdot4041-1=8\,164\,841.\)
Megjegyzés. Sokan az \(\displaystyle x,y\geq0\) esetet számolták össze, szorozták 4-gyel, majd az eredményből kivonták a többször számolt számpárokat (a tengelyeken lévőket kétszer, míg a (0;0) párt négyszer számoltuk így). A számolás:
\(\displaystyle 4\cdot\frac{(1+2021)\cdot2021}{2}-2\cdot4041-1=4\cdot2\,043\,231-8083=8\,164\,841.\)
2. megoldás. Keressük az
\(\displaystyle |x|+|y|<n\)
egyenlőtlenség megoldásainak számát.
Az \(\displaystyle x\) tengely felett lévő (piros) pontok száma:
\(\displaystyle 1+3+...+(1+2\cdot(n-2))=\frac{(1+(2n-3))\cdot(n-1)}{2}=(n-1)^2.\)
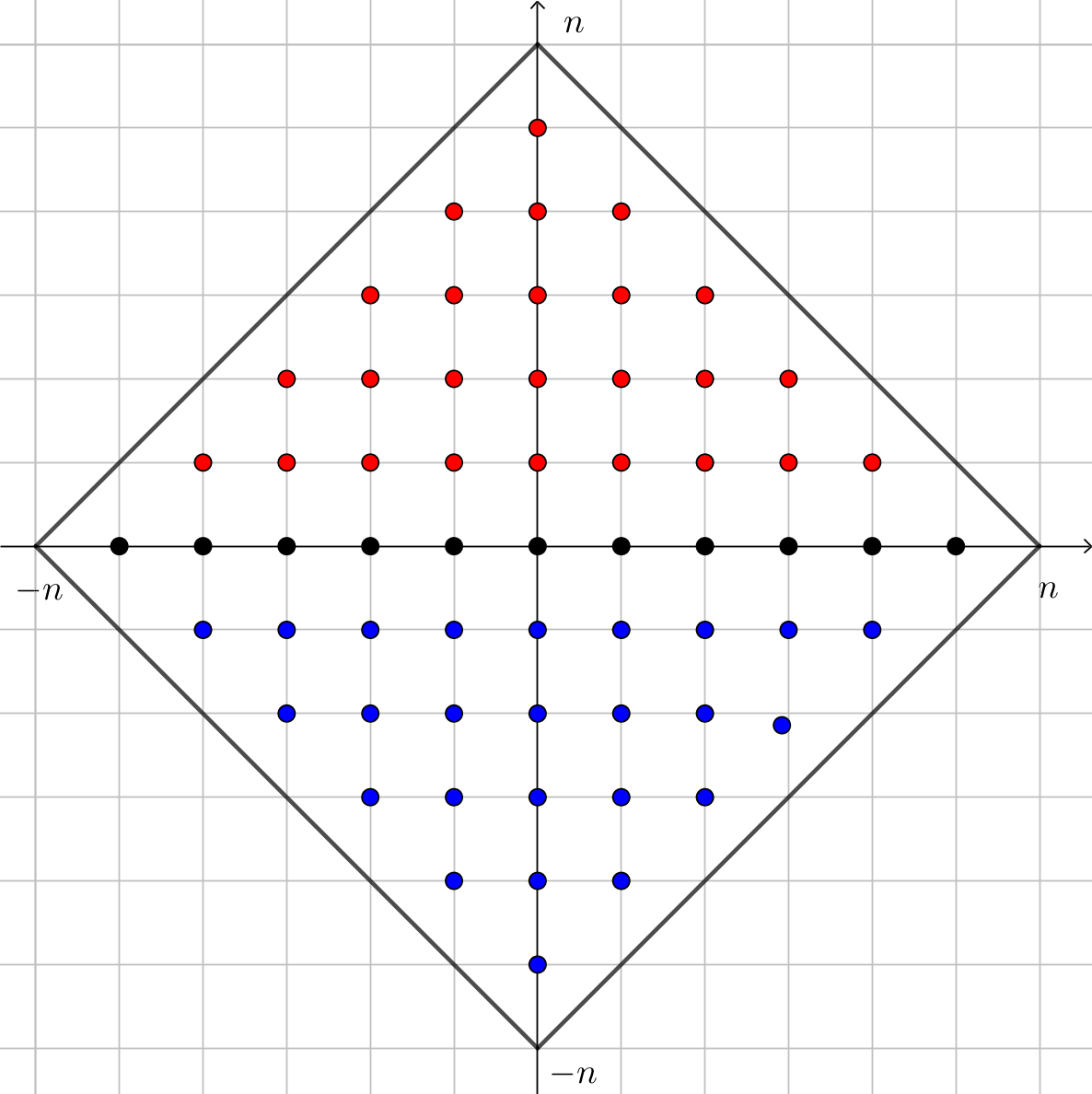
Ennek kétszerese a kék és piros pontok száma együtt: \(\displaystyle 2(n-1)^2\).
Az \(\displaystyle x\) tengelyen lévő (fekete) pontok száma: \(\displaystyle 2(n-1)+1=2n-1\).
Összesen \(\displaystyle 2(n-1)^2+2n-1=2n^2-2n+1\) ilyen számpár van, ami \(\displaystyle n=2021\) esetén \(\displaystyle 2\cdot2021^2-2\cdot2021+1=8\,164\,841\).
3. megoldás. Szemléltessük a pontokat a koordinátarendszerben. Tekintsük a feladatot általánosan: keressük az
\(\displaystyle |x|+|y|<n\)
egyenlőtlenség megoldásait az egész számpárok körében.
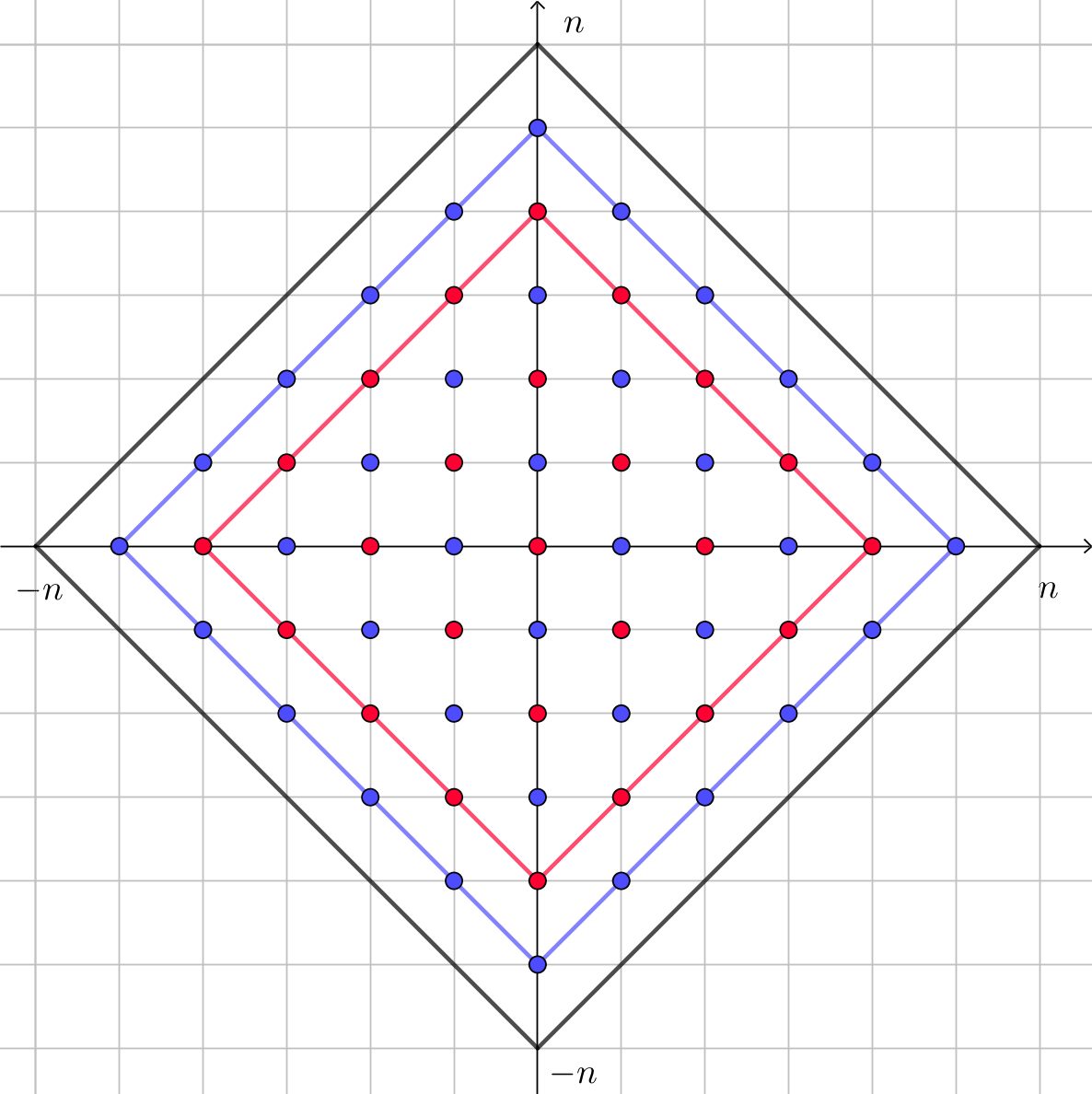
A megoldások két ,,ferde rácsnégyzet'' rácspontjai lesznek, az egyikben kékkel, a másikban pirossal jelöltük a rácspontokat. A kék rácsnégyzet oldalain éppen \(\displaystyle n\) darab rácspont, a piros oldalain pedig \(\displaystyle n-1\) darab rácspont van, így a rácspontok, és így a megfelelő számpárok száma összesen:
\(\displaystyle n^2+(n-1)^2=2021^2+2020^2=8\,164\,841.\)
4. megoldás. Ha \(\displaystyle x,y\) olyan egészek, melyekre \(\displaystyle |x|+|y|<2021\), akkor \(\displaystyle |x|+|y|\) értéke \(\displaystyle 0,1,\dots,2020\) lehet. Legyen most \(\displaystyle 0\leq k\leq 2020\), és határozzuk meg, hány egész számpárra lesz \(\displaystyle |x|+|y|=k\).
Ha \(\displaystyle k=0\), akkor csak egyre: \(\displaystyle (x,y)=(0,0)\) esetén. Ha \(\displaystyle 0<k\) egész szám, akkor \(\displaystyle x\) értékére biztosan \(\displaystyle -k\leq x\leq k\). Ha \(\displaystyle x=k\) vagy \(\displaystyle x=-k\), akkor \(\displaystyle y=0\) kell legyen, ha pedig \(\displaystyle -k<x<k\), akkor \(\displaystyle y=k-|x|\) és \(\displaystyle y=|x|-k\) lesznek megfelelők. Így két olyan \(\displaystyle x\) érték van, amihez egyetlen megfelelő \(\displaystyle y\) található, és \(\displaystyle 2k-1\) olyan \(\displaystyle x\) érték van, melyhez kettő-kettő megfelelő \(\displaystyle y\) található. Vagyis az \(\displaystyle |x|+|y|=k\) egyenlet egész megoldásainak száma \(\displaystyle 2\cdot 1+(2k-1)\cdot 2=4k\).
Ezek alapján az \(\displaystyle |x|+|y|<2021\) egyenlőtlenség egész megoldásainak száma \(\displaystyle 1+4+8+\dots+4\cdot 2020=1+4\cdot \frac{2020\cdot 2021}{2}=8\,164\,841\).
Statistics:
186 students sent a solution. 5 points: 93 students. 4 points: 22 students. 3 points: 15 students. 2 points: 9 students. 1 point: 8 students. 0 point: 25 students. Unfair, not evaluated: 12 solutionss. Not shown because of missing birth date or parental permission: 2 solutions.
Problems in Mathematics of KöMaL, February 2021
