 Problem C. 1654. (February 2021)
Problem C. 1654. (February 2021)
C. 1654. Find the radius of each circle that is tangent to the graphs of the functions \(\displaystyle f(x)=\frac{3x-6}{4}\) and \(\displaystyle g(x)=\frac{28-4x}{3}\), and also touches the \(\displaystyle x\)-axis.
(5 pont)
Deadline expired on March 10, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az \(\displaystyle f(x)\) és \(\displaystyle g(x)\) függvények képe a derékszögű koordináta-rendszerben egy-egy egyenes, legyenek ezek rendre \(\displaystyle f\) és \(\displaystyle g\). A függvények hozzárendelési szabályából leolvashatóan az \(\displaystyle f\) és \(\displaystyle g\) egyenesek meredeksége:
\(\displaystyle m_f=\frac{3}{4};\qquad{m_g=-\frac{4}{3}}.\)
Ha két egyenesnek létezik meredeksége, akkor a két egyenes pontosan akkor merőleges egymásra, ha a meredekségeik szorzata \(\displaystyle -1\). Ez a feladatbeli két egyenesnél fennáll, hiszen
\(\displaystyle m_f\cdot{m_g}=\frac{3}{4}\cdot\Bigg(-\frac{4}{3}\Bigg)=-1.\)
Legyenek az \(\displaystyle f\) és \(\displaystyle g\) egyenesnek az \(\displaystyle x\) tengellyel való metszéspontjai rendre \(\displaystyle A\) és \(\displaystyle B\), a két egyenes metszéspontja pedig \(\displaystyle C\).
A
\(\displaystyle \frac{3x-6}{4}=0;\qquad{\frac{28-4x}{3}=0}\)
egyenletekből azt kapjuk, hogy az \(\displaystyle A\), illetve \(\displaystyle B\) pontok koordinátái:
| \(\displaystyle (1)\) | \(\displaystyle A(2;0);\qquad{B(7;0)}.\) |
A
\(\displaystyle \frac{3x-6}{4}=\frac{28-4x}{3}\)
egyenlet megoldása \(\displaystyle x=5,2\), ez a \(\displaystyle C\) pont első koordinátája, innen visszahelyettesítéssel kapjuk a \(\displaystyle C\) pont második koordinátáját. Így
| \(\displaystyle (2)\) | \(\displaystyle C(5,2;\;{2,4}).\) |
Tekintsük most a feladat feltételeinek megfelelő ábrát.
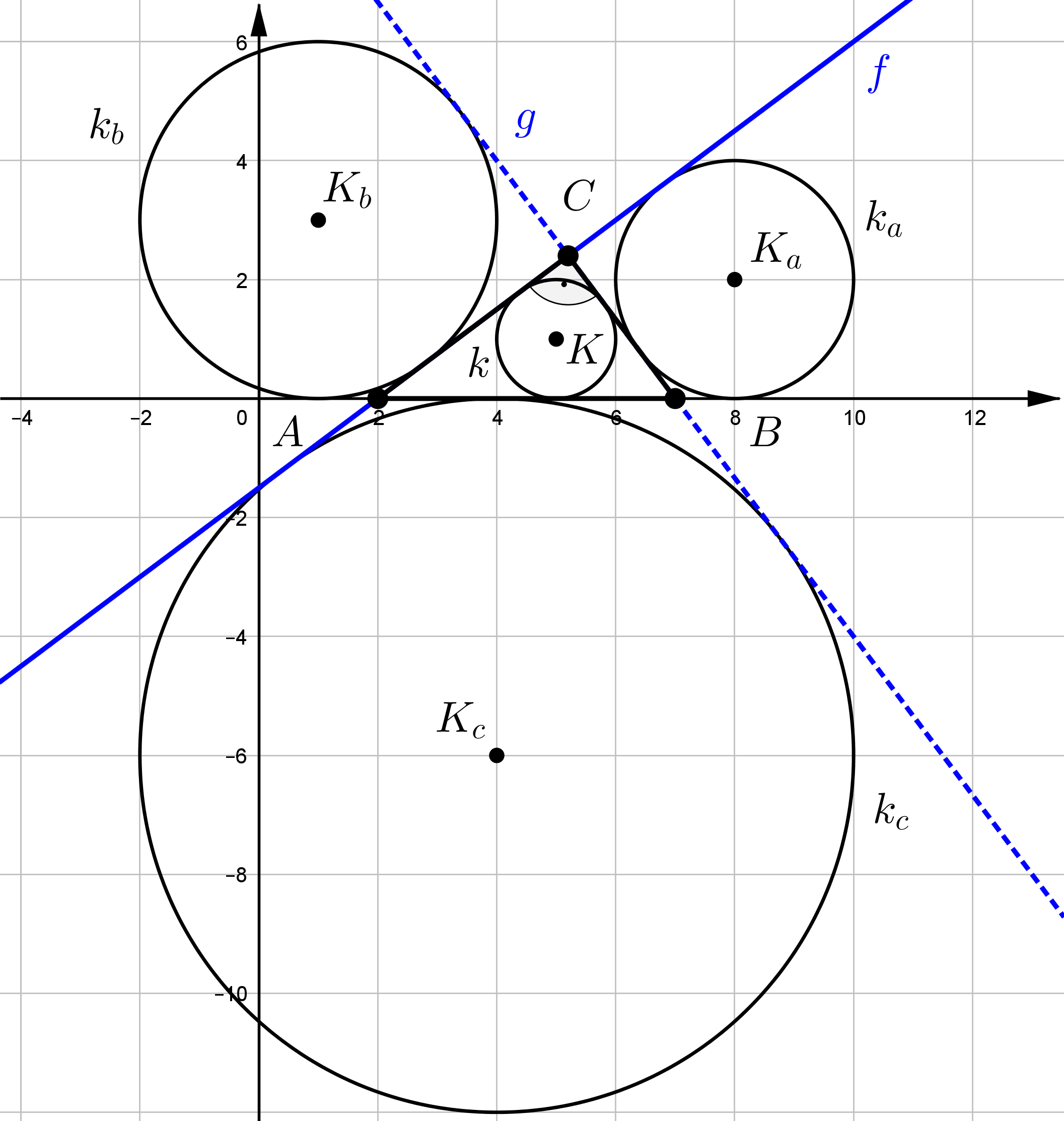
A továbbiakban kiszámítjuk az \(\displaystyle ABC\) derékszögű háromszög oldalainak hosszát és a háromszög területét. Az ábrából könyen leolvasható, hogy \(\displaystyle AB=5\). A \(\displaystyle BC\) távolságot a két, koordinátáival adott pont távolságképletéből kapjuk:
\(\displaystyle BC=\sqrt{(7-5,2)^2+(0-2,4)^2}=3,\)
így az \(\displaystyle AC\) távolság a Pitagorasz-tétel alkalmazásával:
\(\displaystyle AC=4.\)
Eredményeink segítségével megadhatjuk az \(\displaystyle ABC\) háromszög kerületét és területét:
\(\displaystyle K_{ABC}=12;\qquad T_{ABC}=6.\)
A feladatban szereplő függvények grafikonját és az \(\displaystyle x\) tengelyt érintő körök nem mások, mint az \(\displaystyle ABC\) háromszög \(\displaystyle K\) középpontú beírt köre és az oldalaihoz hozzáírt, \(\displaystyle K_a, K_b, K_c\) középpontú körök. A körök sugarai, mint ismeretes
\(\displaystyle r=\frac{T_{ABC}}{s},\qquad{R_a=\frac{T_{ABC}}{s-a}},\qquad{R_b=\frac{T_{ABC}}{s-b}},\qquad{R_c=\frac{T_{ABC}}{s-c}},\)
ahol \(\displaystyle s=6\) az \(\displaystyle ABC\) háromszög félkerülete. A terület és a kerület ismeretében ezek egyszerűen kiszámíthatók:
\(\displaystyle r=6/6=1,\qquad{R_a=6/3=2},\qquad{R_b=6/2=3},\qquad{R_c=6/1=6}.\)
Statistics:
125 students sent a solution. 5 points: 74 students. 4 points: 18 students. 3 points: 11 students. 2 points: 5 students. 1 point: 5 students. 0 point: 9 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, February 2021
