 |
A C. 1666. feladat (2021. április) |
C. 1666. Az \(\displaystyle ABC\) hegyesszögű háromszög \(\displaystyle A\) pontból induló belső szögfelezőjének metszéspontja a \(\displaystyle B\)-ből induló belső szögfelezővel, valamint a \(\displaystyle BC\) oldallal \(\displaystyle K\), illetve \(\displaystyle D\). Az \(\displaystyle A\) pontból induló belső szögfelező metszéspontja a \(\displaystyle B\)-ből induló belső szögfelezővel, valamint a \(\displaystyle BC\) oldallal \(\displaystyle K\), illetve \(\displaystyle D\). Az \(\displaystyle AD\) szögfelezőre a \(\displaystyle K\) pontban állított merőleges az \(\displaystyle AB\) oldalt az \(\displaystyle E\) pontban metszi. Az \(\displaystyle E\) pontból a \(\displaystyle BC\)-re állított merőleges talppontja \(\displaystyle F\). Bocsássunk merőlegest a \(\displaystyle D\) pontból az \(\displaystyle AB\) egyenesre, a merőleges talppontja \(\displaystyle T\). Bizonyítsuk be, hogy \(\displaystyle T\) pont illeszkedik a \(\displaystyle KEF\) háromszög körülírt körére.
(5 pont)
A beküldési határidő 2021. május 10-én LEJÁRT.
Megoldás. Tekintsük a feladat feltételeinek megfelelően készített ábrát. A \(\displaystyle K\) pont az \(\displaystyle ABC\) háromszög beírt körének középpontja, és ez a pont az \(\displaystyle ABC\) háromszög belső pontja.
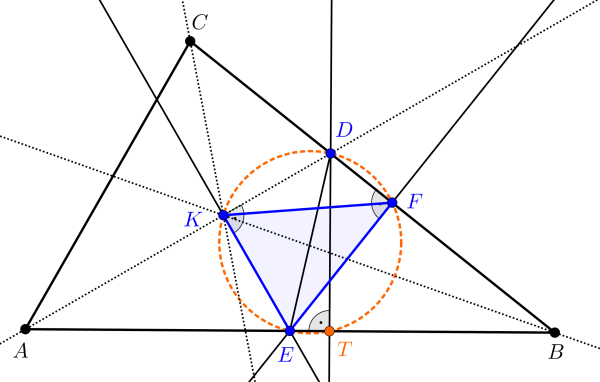
A feladatban leírt konstrukció során keletkezett \(\displaystyle KEF\) háromszög minden esetben létrejön, hiszen az \(\displaystyle EK\) és \(\displaystyle EF\) egyenesek különböznek egymástól.
A \(\displaystyle DE\) szakasz a nyilván különböző \(\displaystyle K\) és \(\displaystyle F\) pontokból derékszögben látszik, ezért a Thalész-tétel megfordítása szerint a \(\displaystyle K\) és \(\displaystyle F\) pontok illeszkednek a \(\displaystyle DE\) átmérőjű körre, ez a kör a \(\displaystyle KEF\) háromszög körülírt köre.
A \(\displaystyle DE\), mint átmérő fölé rajzolt kör tartalmazza az \(\displaystyle ABC\) háromszög síkjának mindazon pontjait, amelyekből a \(\displaystyle DE\) szakasz derékszögben látszik, tehát a \(\displaystyle T\) pontot is. Eszerint a \(\displaystyle D\) pontból az \(\displaystyle AB\)-re bocsátott merőleges \(\displaystyle T\) talppontja valóban illeszkedik a \(\displaystyle KEF\) háromszög körülírt körére.
Statisztika:
57 dolgozat érkezett. 5 pontot kapott: Bencz Benedek, Besze Zsolt, Böröczky András Bálint, Cynolter Dorottya, Deák Gergely, Deme Erik, Fehérvári Donát, Fekete Patrik, Ferenc Ákos, Horváth Milán, Hosszu Noel, Iványi Zsolt, Keszthelyi Eszter, Kiss 625 Dóra, Kovács Benedek Noel, Kurucz Márton, Lőrincz László Lénárd, Lőw László, Molnár Kristóf, Novák Zalán Zoltán, Pekk Márton, Sipos Dorka, Szabó Réka, Szabó Zóra, Tomesz László Gergő, Tóth Gréta, Zádori Petra, Zupkó Bence Kristóf. 4 pontot kapott: Barát Benedek, Borsos Balázs, Foris Dávid, Gecseg Bence, Győrffy Nándor, Han Ziying, Nagy 123 Krisztina, Radzik Réka, Rózsa Félix, Schneider Dávid, Simon 456 Dániel, Sipeki Márton, Szakács Domonkos, Szamkó Szabolcs, Vankó Lóránt Albert, Vincze Farkas Csongor, Werner Kinga, Wrana Gergő, Zentai Zoé. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2021. áprilisi matematika feladatai

