 |
A C. 1675. feladat (2021. május) |
C. 1675. Az \(\displaystyle ABC\) háromszög \(\displaystyle AB\) oldalának egy \(\displaystyle D\) belső pontjára
\(\displaystyle \frac{AD}{DB}=\frac{m}{n}<\frac{1}{2}, \)
ahol \(\displaystyle m\), \(\displaystyle n\) pozitív számok. Az \(\displaystyle E\) pont a háromszög kerületének egy, a \(\displaystyle D\)-től különböző pontja úgy, hogy a \(\displaystyle DE\) egyenes a háromszög területét \(\displaystyle 1:2\) arányú részekre osztja. Adjuk meg, hogy az \(\displaystyle m\) és \(\displaystyle n\) számoktól függően az \(\displaystyle E\) pont mely oldalra esik és milyen arányban osztja azt.
(5 pont)
A beküldési határidő 2021. június 10-én LEJÁRT.
1. megoldás. Legyen az \(\displaystyle AB\) oldal \(\displaystyle A\)-hoz közelebbi harmadolópontja \(\displaystyle H\). Mivel a feltétel szerint \(\displaystyle \frac{AD}{DB}=\frac{m}{n}<\frac{1}{2}\), ezért \(\displaystyle D\) az \(\displaystyle AH\) szakasz belső pontja. Tekintsük a következő ábrát.
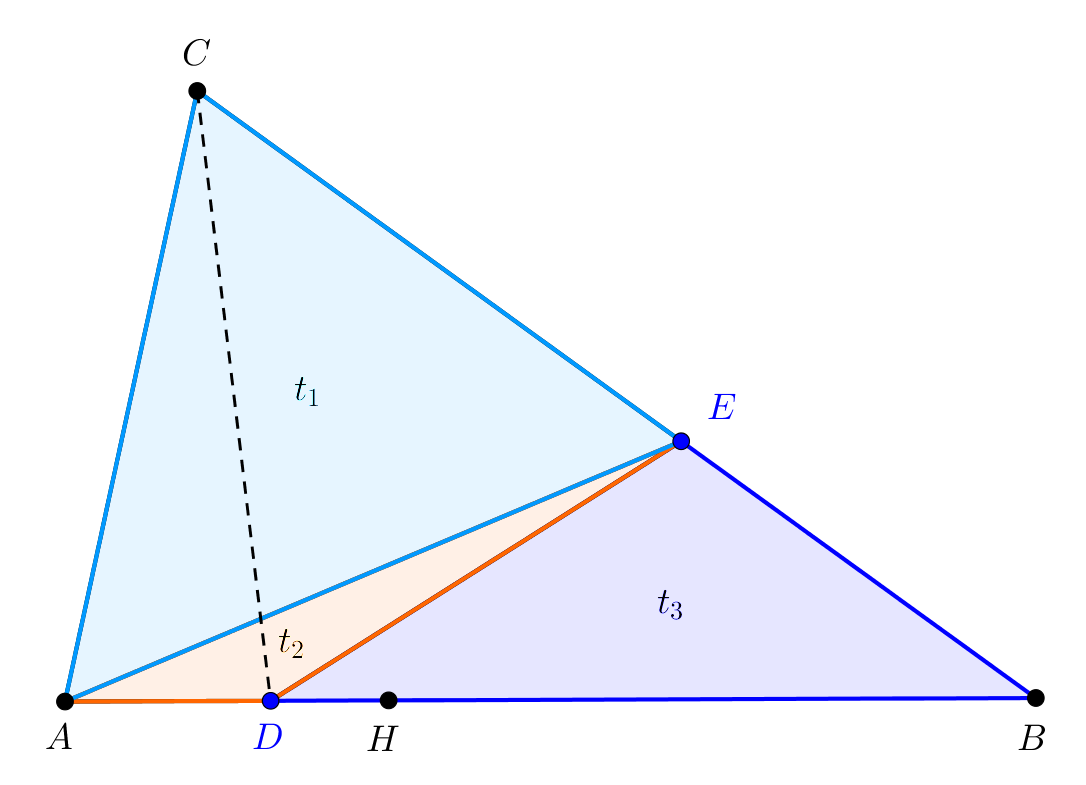
Az \(\displaystyle AHC\) és \(\displaystyle ABC\) háromszögek \(\displaystyle C\) csúcshoz tartozó magassága közös, ezért a két háromszög területének aránya az \(\displaystyle AH\) és \(\displaystyle AB\) alapok hosszának arányával egyenlő, és így
\(\displaystyle \frac{T_{AHC}}{T_{ABC}}=\frac{1}{3},\)
azaz \(\displaystyle T_{AHC}\) az \(\displaystyle ABC\) háromszög területének éppen a harmadrésze. Ebből az következik, hogy a \(\displaystyle CH\) egyenes az \(\displaystyle ABC\) háromszög területét \(\displaystyle 1:2\) arányban osztja.
Az előzőek szerint \(\displaystyle D\) az \(\displaystyle AH\) szakasz belső pontja, így az \(\displaystyle ADC\) háromszög területe \(\displaystyle \frac{T_{ABC}}{3}\)-nál kisebb, vagyis a \(\displaystyle CD\) egyenes nem osztja az \(\displaystyle ABC\) háromszög területét \(\displaystyle 1:2\) arányban, így a keresett \(\displaystyle E\) pont nem azonos a \(\displaystyle C\) ponttal.
De akkor az \(\displaystyle E\) pont nem lehet a \(\displaystyle CA\) oldalon sem, hiszen az így létrejött háromszögek területe az \(\displaystyle ADC\) háromszög területénél is kisebb.
Ezért az \(\displaystyle E\) pont csakis a \(\displaystyle BC\) oldal belső pontja lehet.
Az ábrán az \(\displaystyle AEC, ADE, DBE\) háromszögek területét rendre \(\displaystyle t_1, t_2, t_3\)-mal jelöltük. A \(\displaystyle DE\) egyenes akkor osztja az \(\displaystyle ABC\) háromszög területét \(\displaystyle 1:2\) arányban, ha
| \(\displaystyle (1)\) | \(\displaystyle \frac{t_3}{t_1+t_2}=\frac{1}{2}\) |
vagy, ha
| \(\displaystyle (2)\) | \(\displaystyle \frac{t_3}{t_1+t_2}=\frac{2}{1}.\) |
Vizsgáljuk először az (1) egyenlőséget.
A bal oldalon szereplő tört számlálóját és nevezőjét a pozitív \(\displaystyle t_2\) számmal osztva azt kapjuk, hogy
\(\displaystyle \frac{\frac{t_3}{t_2}}{\frac{t_1}{t_2}+1}=\frac{1}{2}.\)
A \(\displaystyle DBE\) és \(\displaystyle ADE\) háromszögek \(\displaystyle E\) csúcshoz tartozó magassága azonos, ezért területeik aránya az \(\displaystyle DB\) és \(\displaystyle AD\) szakaszok hosszának arányával, vagyis \(\displaystyle \frac{n}{m}\)-nel egyenlő, ezért az előző összefüggés így is írható:
\(\displaystyle \frac{\frac{n}{m}}{{\frac{t_1}{t_2}+1}}=\frac{1}{2},\)
ahonnan
| \(\displaystyle (3)\) | \(\displaystyle \frac{t_1}{t_2}=\frac{2n-m}{m}\) |
következik.
A \(\displaystyle CAE\) és \(\displaystyle ABE\) háromszögek területének aránya a \(\displaystyle CE\) és \(\displaystyle EB\) szakaszok arányával megegyező, mert a két háromszögnek az \(\displaystyle A\) csúcshoz tartozó magassága megegyezik. Ebből azt kapjuk, hogy
\(\displaystyle \frac{CE}{EB}=\frac{t_1}{t_2+t_3}.\)
A kapott egyenlőségben a jobb oldali tört számlálóját és nevezőjét \(\displaystyle t_2\)-vel osztva:
\(\displaystyle \frac{CE}{EB}=\frac{\frac{t_1}{t_2}}{\frac{t_3}{t_2}+1}.\)
Mivel \(\displaystyle \frac{t_3}{t_2}=\frac{n}{m}\), ezért (3) felhasználásával azt kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \frac{CE}{EB}=\frac{2n-m}{m+n}.\) |
A (2) egyenlőséget vizsgálva hasonlóan egyszerűen juthatunk el ahhoz, hogy
\(\displaystyle \frac{\frac{t_3}{t_2}}{\frac{t_1}{t_2}+1}=2,\)
amiből
\(\displaystyle \frac{t_1}{t_2}=\frac{n-2m}{2m},\)
és így ebben az esetben az \(\displaystyle E\) pont a \(\displaystyle BC\) oldalt
| \(\displaystyle (5)\) | \(\displaystyle \frac{CE}{EB}=\frac{n-2m}{2\cdot(m+n)}\) |
arányban osztja.
A feltételekből adódik, hogy a (4) és (5) arányok mindegyike pozitív szám, továbbá az is, hogy az ezeknek megfelelő \(\displaystyle E\) pontok nem azonosak. Ha ugyanis (4) és (5) jobb oldala egyenlő volna, akkor egyszerű számolással belátható módon az \(\displaystyle n=0\) eredményre jutnánk, ez pedig ellenkezik azzal a feltétellel, hogy \(\displaystyle n>0\).
2. megoldás. Ebben a megoldásban eljárást adunk az előzőleg kapott kétféle \(\displaystyle E\) pont megszerkesztésére is.
Az első megoldásban látott módon igazolhatjuk, hogy az \(\displaystyle E\) pont csak a \(\displaystyle BC\) oldal belső pontja lehet.
Tekintsük a következő ábrát, ahol az \(\displaystyle AB\) oldal \(\displaystyle F\) felezőpontján keresztül párhuzamost rajzoltunk a \(\displaystyle CD\)-vel, ez a párhuzamos a \(\displaystyle BC\) szakaszt az \(\displaystyle E'\) pontban metszi. A \(\displaystyle CF\) és \(\displaystyle DE'\) egyenesek metszéspontját \(\displaystyle M\)-mel jelöljük.
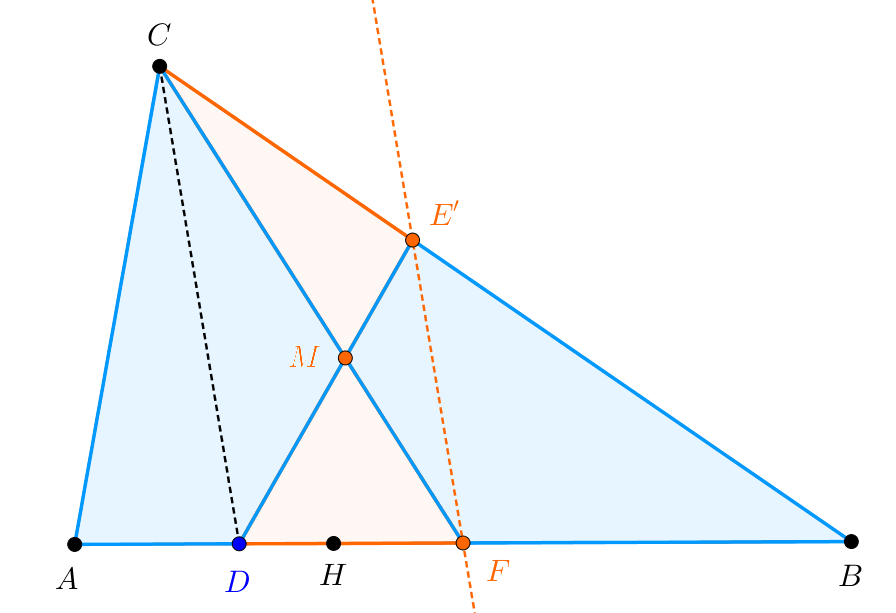
1. ábra
A konstrukció miatt a \(\displaystyle CDFE'\) négyszög trapéz, amelyben a \(\displaystyle CDF\) és \(\displaystyle CDE'\) háromszögek területe egyenlő, hiszen a közös \(\displaystyle CD\) alaphoz tartozó magasságaik hossza a \(\displaystyle CD\) és \(\displaystyle E'F\) párhuzamossága miatt megegyezik. Ebből az is látható, hogy az ábra \(\displaystyle CME'\) és \(\displaystyle DFM\) háromszögeinek területe egyenlő. Mivel az \(\displaystyle ABC\) háromszög \(\displaystyle CF\) súlyvonala felezi a háromszög területét, ezért az \(\displaystyle ADMC\) és \(\displaystyle BE'MF\) négyszögek területe megegyezik.
Mindebből az is következik, hogy a \(\displaystyle DE'\) egyenes felezi az \(\displaystyle ABC\) háromszög területét, vagyis a \(\displaystyle T_{ABC}=T\) jelöléssel:
| \(\displaystyle (1)\) | \(\displaystyle T_{DBE'}=T_{CADE'}=\frac{T}{2}.\) |
Vizsgáljuk most a 2. ábrát, amelyen a \(\displaystyle BE'\) szakasz \(\displaystyle E'\)-höz közelebbi harmadolópontja \(\displaystyle E_1\), ennek az \(\displaystyle E'\)-re vonatkozó tükörképe pedig \(\displaystyle E_2\).

2. ábra
A \(\displaystyle DE_1E'\) háromszög területe a \(\displaystyle DBE'\) háromszög területének harmada, vagyis \(\displaystyle T_{DE_1E'}=\frac{T}{6}\) és ezért (1) alapján egyszerű számolással azt kapjuk, hogy
\(\displaystyle T_{DBE_1}=\frac{T}{3};\qquad{T_{CADE_1}=\frac{2T}{3}}.\)
Ebből pedig azonnal következik, hogy
\(\displaystyle \frac{T_{DBE_1}}{T_{CADE_1}}=\frac{1}{2},\)
tehát \(\displaystyle DE_1\) az egyik olyan egyenes, amely az \(\displaystyle ABC\) háromszög területét \(\displaystyle 1:2\) arányú részekre osztja.
Nyilvánvaló, hogy \(\displaystyle T_{DE_2E'}=\frac{T}{6}\) is igaz, ezért (1) szerint
\(\displaystyle \frac{T_{DBE_2}}{T_{CADE_2}}=\frac{2}{1}\)
is fennáll.
Az első megoldásban láttuk, hogy \(\displaystyle T_{ADC}<\frac{T}{3}\), és mivel most \(\displaystyle T_{CADE_2}=\frac{T}{3}\), ezért az \(\displaystyle E_2\) pont biztosan a \(\displaystyle BC\) szakasz belső pontja.
Azt kaptuk tehát, hogy \(\displaystyle DE_2\) a másik olyan egyenes, amely az \(\displaystyle ABC\) háromszög területét \(\displaystyle 1:2\) arányú részekre osztja.
Az \(\displaystyle \frac{AD}{DB}=\frac{m}{n}\) feltétel szerint \(\displaystyle AD=DB\cdot{\frac{m}{n}}\), és így az \(\displaystyle AD+DB=AB=c\) egyenlőség alapján \(\displaystyle DB\cdot{\frac{m}{n}}+DB=c\), ahonnan \(\displaystyle DB=\frac{n\cdot{c}}{m+n}\).
Mivel \(\displaystyle F\) az \(\displaystyle AB\) oldal felezőpontja, ezért \(\displaystyle DF=DB-\frac{c}{2}\) miatt
| \(\displaystyle (2)\) | \(\displaystyle DF=\frac{c\cdot(n-m)}{2\cdot(m+n)}.\) |
A párhuzamos szelők tétele szerint \(\displaystyle \frac{CE'}{BE'}=\frac{DF}{BF}\), és mivel \(\displaystyle BF=\frac{c}{2}\), ezért (2) felhasználásával
| \(\displaystyle (3).\) | \(\displaystyle \frac{CE'}{BE'}=\frac{n-m}{m+n}.\) |
Ugyanakkor
\(\displaystyle \frac{CE_1}{BE_1}=\frac{CE'+\frac{1}{3}BE'}{\frac{2}{3}BE'}=\frac{3}{2}\frac{CE'}{BE'}+\frac{1}{2},\)
ezért (3) alapján a műveletek elvégzése után azt kapjuk, hogy
| \(\displaystyle (4)\) | \(\displaystyle \frac{CE_1}{BE_1}=\frac{2n-m}{m+n}.\) |
Hasonlóképpen járunk el az \(\displaystyle E_2\) pont esetén is:
\(\displaystyle \frac{CE_2}{BE_2}=\frac{CE'-\frac{1}{3}BE'}{\frac{4}{3}BE'}=\frac{3}{4}\frac{CE'}{BE'}-\frac{1}{4},\)
ahonnan (3)-at ismét felhasználva
| \(\displaystyle (5)\) | \(\displaystyle \frac{CE_2}{BE_2}=\frac{n-2m}{2\cdot(m+n)}.\) |
Eredményeink megegyeznek az első megoldásban kapott arányokkal, mindkét arány a feltételek miatt pozitív, valamint a két arány értékének egyenlősége \(\displaystyle n=0\)-ra vezetne, ezért ez nem lehetséges.
Statisztika:
51 dolgozat érkezett. 5 pontot kapott: Andó Lujza, Bencz Benedek, Besze Zsolt, Cynolter Dorottya, Dobi Dorina Lili, Fekete András Albert, Flódung Áron , Horváth 828 Mátyás, Horváth Milán, Hosszu Noel, Keszthelyi Eszter, Molnár Kristóf, Molnár Réka, Németh László Csaba, Szabó Réka, Szabó Zóra, Szakács Domonkos, Szalanics Tamás, Tóth Gréta, Vitálos Tünde, Xu Yiling, Zaránd Andris. 4 pontot kapott: Biró 424 Ádám, Borsos Balázs, Csilling Dániel, Deák Gergely, Féger Tamás, Fehérvári Donát, Foris Dávid, Josepovits Gábor, Kovács Benedek Noel, Nagy 123 Krisztina, Németh Máté Előd, Radzik Réka, Schneider Anna, Schneider Dávid, Sipeki Márton, Tomesz László Gergő, Werner Kinga. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2021. májusi matematika feladatai

