 |
A C. 1682. feladat (2021. szeptember) |
C. 1682. Egy egységnyi élhosszúságú kocka csúcsai \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) az ábra szerint. Az \(\displaystyle ABDE\) és \(\displaystyle GCFH\) tetraédereket levágjuk a kockából. Mekkora az így kapott test felszíne és térfogata?

Javasolta: Zagyva Tiborné (Baja)
(5 pont)
A beküldési határidő 2021. október 11-én LEJÁRT.
Megoldás. Az \(\displaystyle ABDE\) tetraéder páronként egymásra merőleges éleinek hossza \(\displaystyle AB=AD=AE=1\), a tetraéder többi élének hossza \(\displaystyle BD=DE=EB=\sqrt{2}\). Hasonlóképpen a \(\displaystyle GCFH\) tetraéder páronként merőleges élei \(\displaystyle GC=GF=GH=1\), illetve további élei \(\displaystyle HF=FC=CH=\sqrt{2}\). Tekintsük a következő ábrát.
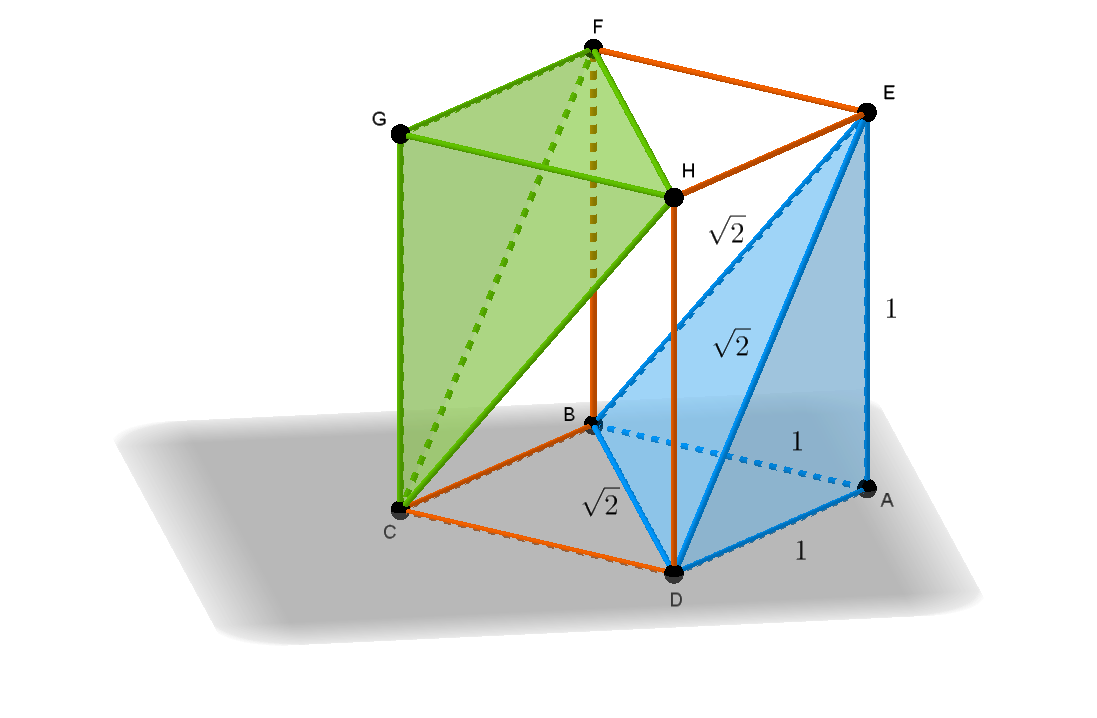
Az egységnyi élű \(\displaystyle ABCDEFGH\) kocka térfogata \(\displaystyle 1\) térfogategység, felszíne \(\displaystyle 6\) darab egységnyi oldalú négyzet területével egyezik meg, tehát \(\displaystyle 6\) területegység. Az \(\displaystyle ABDE\) tetraéder térfogata:
\(\displaystyle V_{ABDE}=\frac{1}{3}\cdot{\frac{AB\cdot{AD}}{2}\cdot{AE}},\)
azaz
| \(\displaystyle (1)\) | \(\displaystyle V_{ABDE}=\frac{1}{6}.\) |
Nyilván ugyanennyi az \(\displaystyle GCFH\) tetraéder térfogata is, hiszen egybevágó az \(\displaystyle ABDE\) tetraéderrel. Ha ezt a két tetraédert levágjuk a kockából, akkor a \(\displaystyle BCDFHE\) ferde hasábot kapjuk, amelynek térfogata (1) alapján
\(\displaystyle V_{BCDFHE}=1-2\cdot{\frac{1}{6}}=\frac{2}{3}\)
térfogategység.
A két tetraéder levágásakor a kocka felszínéből eltávolítunk összesen a kocka három oldallapjának megfelelő területet, azaz \(\displaystyle 3\) területegységet. Ugyanakkor a keletkezett test felszínéhez "hozzáadjuk" a \(\displaystyle \sqrt{2}\) oldalhosszúságú \(\displaystyle BDE\) és \(\displaystyle HFC\) szabályos háromszögek területét. Utóbbi háromszögek területe összesen:
| \(\displaystyle (2)\) | \(\displaystyle 2\cdot{\frac{\sqrt{2}^2\cdot{\sqrt{3}}}{4}}=\sqrt{3}.\) |
Egyszerű számolással kapjuk (2) felhasználásával, hogy a tetraéderek levágása után megmaradt test felszíne:
\(\displaystyle A_{BCDFHE}=6-3+\sqrt{3}=3+\sqrt{3}\)
területegység.
Statisztika:
81 dolgozat érkezett. 5 pontot kapott: Albert Ákos, Bakos Eszter, Besze Zsolt, Biborka Dániel, Cynolter Dorottya, Deák Gergely, Egyházi Hanna, Fekete Patrik, Flódung Áron , Hajós Balázs, Halász Henrik, Horváth 328 Áron, Horváth Milán, Hosszu Noel, Jójárt Emese, Josepovits Gábor, Keszthelyi Eszter, Kiss 625 Dóra, Kurucz Márton, Lajtos Bence Levente, Murai Dóra Eszter, Nagy Daniella, Németh Máté Előd, Pekk Márton, Petneházi Péter, Poluczik Csongor, Rumpler Bianka, Sarkadi Sándor, Schneider Dávid, Sipeki Márton, Süveges Gergő, Szabó 219 Petra, Szabó Réka, Szabó Zóra, Szalanics Tamás, Szittyai Anna, Szpisják Bence Tibor, Tóth Gerda Júlia, Tóth Gréta, Török Dalma, Váczy Dorottya, Vass Boldizsár, Velkey János, Waldhauser Miklós, Weeber László, Werner Kinga, Xu Yiling. 4 pontot kapott: 18 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2021. szeptemberi matematika feladatai

