 |
A C. 1686. feladat (2021. október) |
C. 1686. Az \(\displaystyle ABC\) derékszögű háromszög átfogója az \(\displaystyle AB\) szakasz. Az \(\displaystyle A\) csúcsból kiinduló \(\displaystyle f\) belső szögfelező a \(\displaystyle BC\) oldalt a \(\displaystyle D\) pontban metszi. Bizonyítsuk be, hogy az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok hosszának mértani közepe éppen az \(\displaystyle f = AD\) szögfelező hossza.
Javasolta: Zagyva Tiborné (Baja)
(5 pont)
A beküldési határidő 2021. november 10-én LEJÁRT.
1. megoldás. Az \(\displaystyle ABC\) háromszög oldalait a szokásos módon jelöljük: \(\displaystyle BC=a, CA=b, AB=c\).
Tekintsük a következő ábrát.
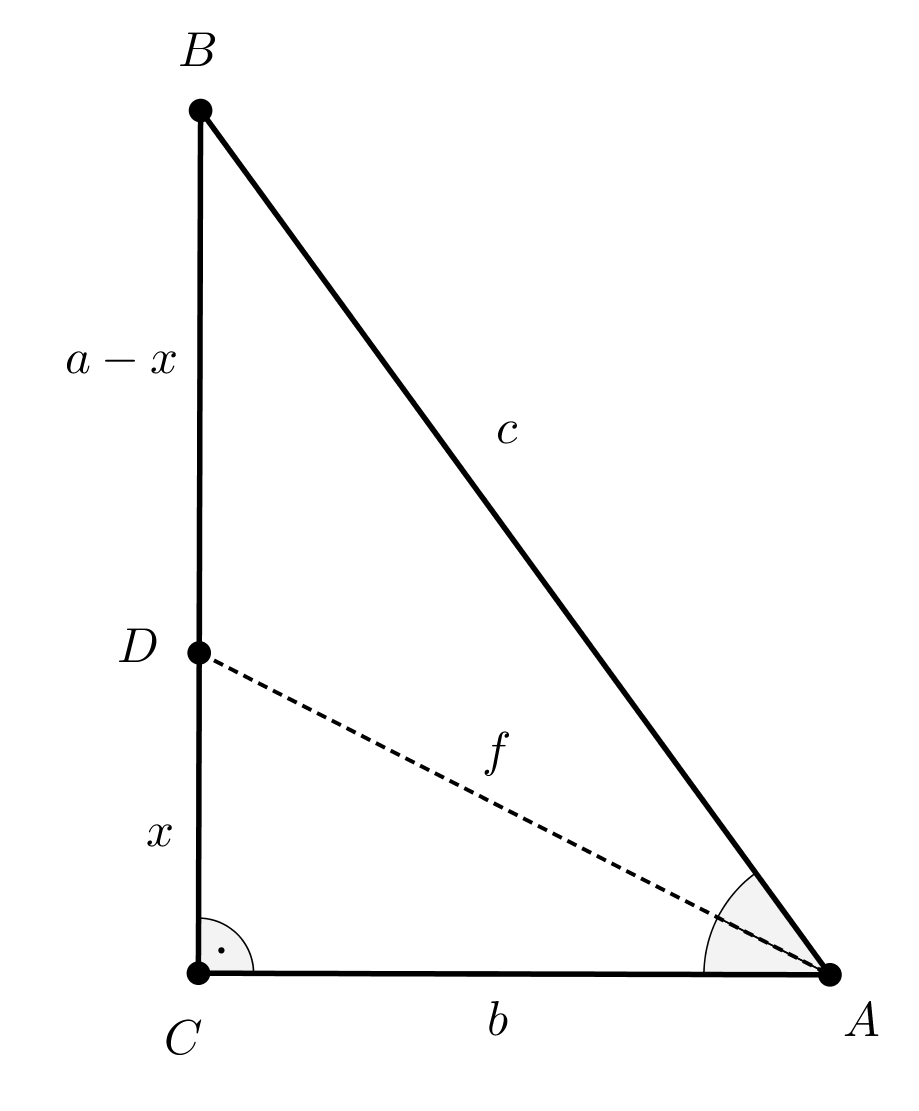
A belső szögfelező tétele szerint:
\(\displaystyle \frac{BD}{DC}=\frac{a-x}{x}=\frac{c}{b}.\)
Ebből az egyenletből a műveletek elvégzésével és rendezéssel megkapjuk a \(\displaystyle DC=x\) és \(\displaystyle BD=a-x\) szakaszok hosszát:
\(\displaystyle ab-bx=cx,\)
\(\displaystyle ab=x(b+c),\)
| \(\displaystyle {(1)}\) | \(\displaystyle x=\frac{ab}{b+c},\) |
| \(\displaystyle {(2)}\) | \(\displaystyle a-x=a-\frac{ab}{b+c}=\frac{ab+ac-ab}{b+c}=\frac{ac}{b+c}.\) |
Az \(\displaystyle ADC\) derékszögű háromszögben felírhatjuk a Pitagorasz-tételt:
\(\displaystyle f^2=x^2+b^2,\)
ahonnan (1) felhasználásával
\(\displaystyle f^2=\frac{a^2b^2}{(b+c)^2}+b^2,\)
majd közös nevezőre hozással és kiemeléssel
\(\displaystyle f^2=\frac{b^2\cdot\big[a^2+(b+c)^2\big]}{(b+c)^2}.\)
A tört számlálójában elvégezzük a műveleteket és felhasználjuk, hogy az \(\displaystyle ABC\) háromszögre felírt Pitagorasz-tétel miatt \(\displaystyle a^2+b^2=c^2\), majd (\(\displaystyle b+c\))-vel egyszerűsítünk:
| \(\displaystyle {(3)}\) | \(\displaystyle f^2=\frac{b^2(a^2+b^2+c^2+2bc)}{(b+c)^2}=\frac{b^2(2c^2+2bc)}{(b+c)^2}=\frac{2b^2c(b+c)}{(b+c)^2}=\frac{2b^2c}{b+c}.\) |
Ezután bizonyítani kell, hogy az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok hosszának mértani közepe megegyezik a (3) egyenlet jobb oldalának négyzetgyökével, azaz a szakaszok szorzata megegyezik az egyenlet jobb oldalán szereplő kifejezéssel.
Ehhez elegendő az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok szorzatát vizsgálni. Nyilvánvaló, hogy \(\displaystyle AB-BD>0\), hiszen \(\displaystyle AB>BC>BD\), mivel \(\displaystyle AB\) az \(\displaystyle ABC\) háromszög átfogója, a \(\displaystyle D\) pont pedig a \(\displaystyle BC\) befogó belső pontja.
(2) és (1) szerint \(\displaystyle AB-BD=c-\frac{ac}{b+c}\), valamint \(\displaystyle AC+CD=b+\frac{ab}{b+c}\), ezért
\(\displaystyle \big(AB-BD\big)\cdot\big(AC+CD\big)=\bigg(c-\frac{ac}{b+c}\bigg)\cdot\bigg(b+\frac{ab}{b+c}\bigg).\)
A törtek közös nevezőre való hozásával, a műveletek elvégzésével és rendezéssel:
\(\displaystyle \big(AB-BD\big)\cdot\big(AC+CD\big)=cb+\frac{abc}{b+c}-\frac{abc}{b+c}-\frac{a^2bc}{(b+c)^2}= \frac{bc\cdot\big[(b+c)^2-a^2\big]}{(b+c)^2},\)
innen pedig, ismét felhasználva az \(\displaystyle a^2+b^2=c^2\) pitagoraszi összefüggést:
| \(\displaystyle {(4)}\) | \(\displaystyle \big(AB-BD\big)\cdot\big(AC+CD\big)=\frac{bc(b^2+c^2+2bc-a^2)}{(b+c)^2}=\frac{bc(2b^2+2bc)}{(b+c)^2}=\frac{2b^2c}{b+c}.\) |
(3) és (4) azt jelenti, hogy \(\displaystyle f^2=\big(AB-BD\big)\cdot\big(AC+CD\big)\), és emiatt
\(\displaystyle f=\sqrt{(AB-BD)\cdot(AC+CD)},\)
ezért az \(\displaystyle f\) szögfelező hossza valóban az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok hosszának mértani közepe.
Megjegyzés
Az \(\displaystyle f^2=\frac{2b^2c}{b+c}=b\cdot{\frac{2bc}{b+c}}\) alakból jól látszik, hogy \(\displaystyle f\) a \(\displaystyle b\) befogó és a \(\displaystyle b, c\) oldalak harmonikus közepének a mértani közepe.
2. megoldás. Tükrözzük a \(\displaystyle D\) pontot a \(\displaystyle B\) csúcsból induló \(\displaystyle BE\) belső szögfelezőre, a szögfelező tulajdonsága miatt a \(\displaystyle D'\) tükörkép az \(\displaystyle AB\) átfogó belső pontja. Jelöljük meg továbbá az \(\displaystyle AC\) egyenesen, a \(\displaystyle C\) ponton túl azt a \(\displaystyle D''\) pontot, amelyre \(\displaystyle CD''=CD\).
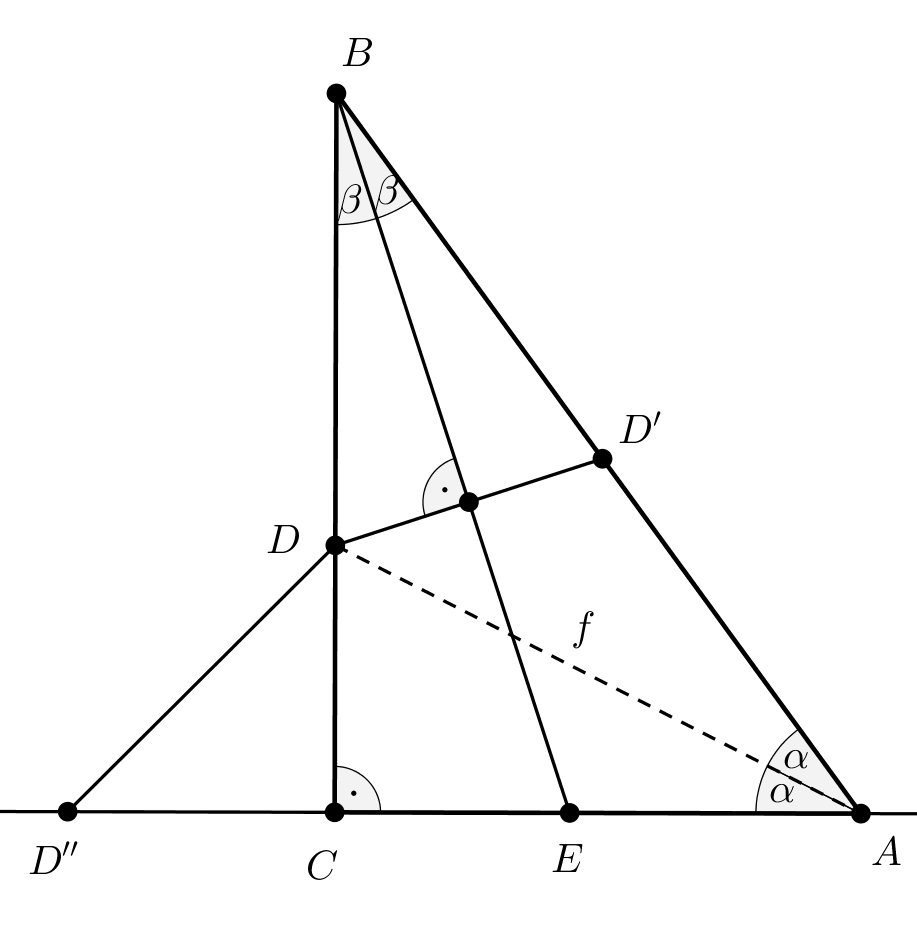
Mivel a tükrözés miatt \(\displaystyle BD=BD'\) ezért egyrészt \(\displaystyle AD'=AB-BD\), másrészt \(\displaystyle AD''=AC+CD\).
Az ábra jelöléseivel \(\displaystyle 2\alpha+2\beta=90^{\circ}\), így \(\displaystyle \alpha+\beta=45^{\circ}\). Egyszerűen belátható, hogy \(\displaystyle BD'D\sphericalangle=90^{\circ}-\beta\), és ezért \(\displaystyle AD'D\sphericalangle=90^{\circ}+\beta\).
A \(\displaystyle DD''C\) egyenlő szárú, derékszögű háromszög, tehát \(\displaystyle D''DC\sphericalangle=45^{\circ}\), és mivel \(\displaystyle ADC\sphericalangle=90^{\circ}-\alpha\), ezért \(\displaystyle ADD''\sphericalangle=90^{\circ}-\alpha+45^{\circ}\), ebből \(\displaystyle \alpha+\beta=45^{\circ}\) alapján \(\displaystyle ADD''\sphericalangle=90^{\circ}+\beta\) következik.
Az \(\displaystyle AD'D\) és \(\displaystyle ADD''\) háromszögek két-két szögének nagysága \(\displaystyle \alpha\) és \(\displaystyle 90^{\circ}+\beta\), így a háromszögek harmadik szöge is nyilván megegyezik, ez pedig azt jelenti, hogy a két háromszög hasonló. Hasonló háromszögekben a megfelelő oldalak aránya megegyezik, ezért
\(\displaystyle \frac{AD'}{AD}=\frac{AD}{AD''},\)
azaz
\(\displaystyle AD^2=AD'\cdot{AD''}.\)
Mivel \(\displaystyle AD=f\), \(\displaystyle AD'=AB-BD\), illetve \(\displaystyle AD''=AC+CD\), előző eredményünkből \(\displaystyle f^2=({AB-BD})\cdot({AC+CD})\) következik, ez éppen a feladat állítása, hiszen ebből a nyilvánvalóan pozitív \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) számok mértani közepe:
\(\displaystyle f=\sqrt{(AB-BD)\cdot(AC+CD)}.\)
Megjegyzés. Könnyen bizonyítható, hogy a feladat állítása tetszőleges háromszögre igaz.
Statisztika:
116 dolgozat érkezett. 5 pontot kapott: 60 versenyző. 4 pontot kapott: 11 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 9 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 8 versenyző. Nem versenyszerű: 1 dolgozat. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2021. októberi matematika feladatai

