 Problem C. 1686. (October 2021)
Problem C. 1686. (October 2021)
C. 1686. The hypotenuse of the right-angled triangle \(\displaystyle ABC\) is \(\displaystyle AB\). The interior angle bisector \(\displaystyle f\) drawn from vertex \(\displaystyle A\) intersects side \(\displaystyle BC\) at point \(\displaystyle D\). Prove that the geometric mean of line segments \(\displaystyle AB-BD\) and \(\displaystyle AC+CD\) equals the length of angle bisector \(\displaystyle f = AD\).
Proposed by N. Zagyva, Baja
(5 pont)
Deadline expired on November 10, 2021.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. Az \(\displaystyle ABC\) háromszög oldalait a szokásos módon jelöljük: \(\displaystyle BC=a, CA=b, AB=c\).
Tekintsük a következő ábrát.
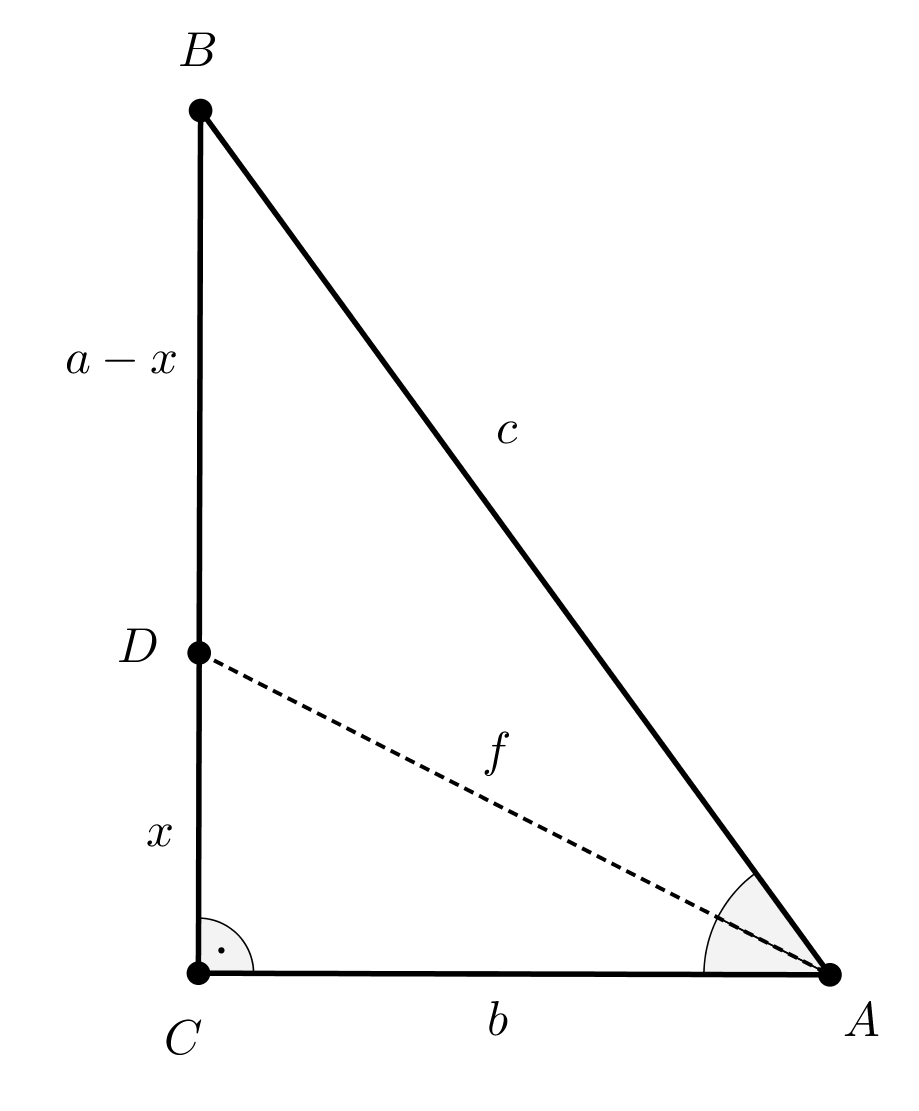
A belső szögfelező tétele szerint:
\(\displaystyle \frac{BD}{DC}=\frac{a-x}{x}=\frac{c}{b}.\)
Ebből az egyenletből a műveletek elvégzésével és rendezéssel megkapjuk a \(\displaystyle DC=x\) és \(\displaystyle BD=a-x\) szakaszok hosszát:
\(\displaystyle ab-bx=cx,\)
\(\displaystyle ab=x(b+c),\)
| \(\displaystyle {(1)}\) | \(\displaystyle x=\frac{ab}{b+c},\) |
| \(\displaystyle {(2)}\) | \(\displaystyle a-x=a-\frac{ab}{b+c}=\frac{ab+ac-ab}{b+c}=\frac{ac}{b+c}.\) |
Az \(\displaystyle ADC\) derékszögű háromszögben felírhatjuk a Pitagorasz-tételt:
\(\displaystyle f^2=x^2+b^2,\)
ahonnan (1) felhasználásával
\(\displaystyle f^2=\frac{a^2b^2}{(b+c)^2}+b^2,\)
majd közös nevezőre hozással és kiemeléssel
\(\displaystyle f^2=\frac{b^2\cdot\big[a^2+(b+c)^2\big]}{(b+c)^2}.\)
A tört számlálójában elvégezzük a műveleteket és felhasználjuk, hogy az \(\displaystyle ABC\) háromszögre felírt Pitagorasz-tétel miatt \(\displaystyle a^2+b^2=c^2\), majd (\(\displaystyle b+c\))-vel egyszerűsítünk:
| \(\displaystyle {(3)}\) | \(\displaystyle f^2=\frac{b^2(a^2+b^2+c^2+2bc)}{(b+c)^2}=\frac{b^2(2c^2+2bc)}{(b+c)^2}=\frac{2b^2c(b+c)}{(b+c)^2}=\frac{2b^2c}{b+c}.\) |
Ezután bizonyítani kell, hogy az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok hosszának mértani közepe megegyezik a (3) egyenlet jobb oldalának négyzetgyökével, azaz a szakaszok szorzata megegyezik az egyenlet jobb oldalán szereplő kifejezéssel.
Ehhez elegendő az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok szorzatát vizsgálni. Nyilvánvaló, hogy \(\displaystyle AB-BD>0\), hiszen \(\displaystyle AB>BC>BD\), mivel \(\displaystyle AB\) az \(\displaystyle ABC\) háromszög átfogója, a \(\displaystyle D\) pont pedig a \(\displaystyle BC\) befogó belső pontja.
(2) és (1) szerint \(\displaystyle AB-BD=c-\frac{ac}{b+c}\), valamint \(\displaystyle AC+CD=b+\frac{ab}{b+c}\), ezért
\(\displaystyle \big(AB-BD\big)\cdot\big(AC+CD\big)=\bigg(c-\frac{ac}{b+c}\bigg)\cdot\bigg(b+\frac{ab}{b+c}\bigg).\)
A törtek közös nevezőre való hozásával, a műveletek elvégzésével és rendezéssel:
\(\displaystyle \big(AB-BD\big)\cdot\big(AC+CD\big)=cb+\frac{abc}{b+c}-\frac{abc}{b+c}-\frac{a^2bc}{(b+c)^2}= \frac{bc\cdot\big[(b+c)^2-a^2\big]}{(b+c)^2},\)
innen pedig, ismét felhasználva az \(\displaystyle a^2+b^2=c^2\) pitagoraszi összefüggést:
| \(\displaystyle {(4)}\) | \(\displaystyle \big(AB-BD\big)\cdot\big(AC+CD\big)=\frac{bc(b^2+c^2+2bc-a^2)}{(b+c)^2}=\frac{bc(2b^2+2bc)}{(b+c)^2}=\frac{2b^2c}{b+c}.\) |
(3) és (4) azt jelenti, hogy \(\displaystyle f^2=\big(AB-BD\big)\cdot\big(AC+CD\big)\), és emiatt
\(\displaystyle f=\sqrt{(AB-BD)\cdot(AC+CD)},\)
ezért az \(\displaystyle f\) szögfelező hossza valóban az \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) szakaszok hosszának mértani közepe.
Megjegyzés
Az \(\displaystyle f^2=\frac{2b^2c}{b+c}=b\cdot{\frac{2bc}{b+c}}\) alakból jól látszik, hogy \(\displaystyle f\) a \(\displaystyle b\) befogó és a \(\displaystyle b, c\) oldalak harmonikus közepének a mértani közepe.
2. megoldás. Tükrözzük a \(\displaystyle D\) pontot a \(\displaystyle B\) csúcsból induló \(\displaystyle BE\) belső szögfelezőre, a szögfelező tulajdonsága miatt a \(\displaystyle D'\) tükörkép az \(\displaystyle AB\) átfogó belső pontja. Jelöljük meg továbbá az \(\displaystyle AC\) egyenesen, a \(\displaystyle C\) ponton túl azt a \(\displaystyle D''\) pontot, amelyre \(\displaystyle CD''=CD\).
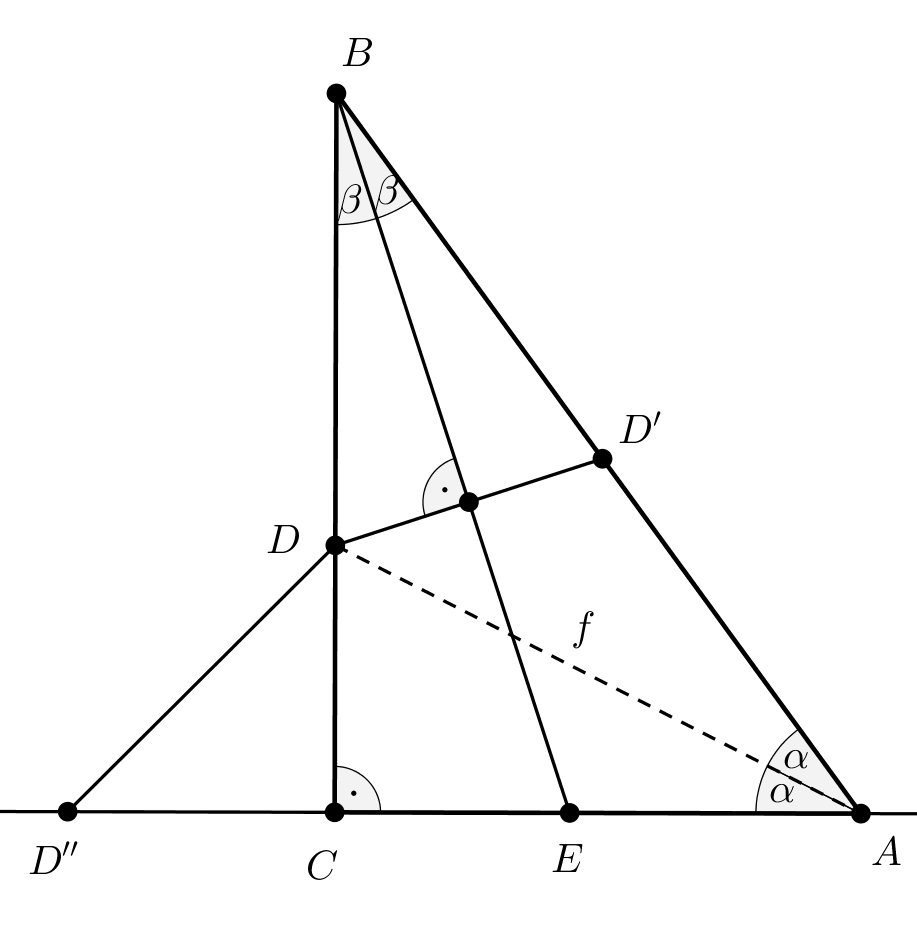
Mivel a tükrözés miatt \(\displaystyle BD=BD'\) ezért egyrészt \(\displaystyle AD'=AB-BD\), másrészt \(\displaystyle AD''=AC+CD\).
Az ábra jelöléseivel \(\displaystyle 2\alpha+2\beta=90^{\circ}\), így \(\displaystyle \alpha+\beta=45^{\circ}\). Egyszerűen belátható, hogy \(\displaystyle BD'D\sphericalangle=90^{\circ}-\beta\), és ezért \(\displaystyle AD'D\sphericalangle=90^{\circ}+\beta\).
A \(\displaystyle DD''C\) egyenlő szárú, derékszögű háromszög, tehát \(\displaystyle D''DC\sphericalangle=45^{\circ}\), és mivel \(\displaystyle ADC\sphericalangle=90^{\circ}-\alpha\), ezért \(\displaystyle ADD''\sphericalangle=90^{\circ}-\alpha+45^{\circ}\), ebből \(\displaystyle \alpha+\beta=45^{\circ}\) alapján \(\displaystyle ADD''\sphericalangle=90^{\circ}+\beta\) következik.
Az \(\displaystyle AD'D\) és \(\displaystyle ADD''\) háromszögek két-két szögének nagysága \(\displaystyle \alpha\) és \(\displaystyle 90^{\circ}+\beta\), így a háromszögek harmadik szöge is nyilván megegyezik, ez pedig azt jelenti, hogy a két háromszög hasonló. Hasonló háromszögekben a megfelelő oldalak aránya megegyezik, ezért
\(\displaystyle \frac{AD'}{AD}=\frac{AD}{AD''},\)
azaz
\(\displaystyle AD^2=AD'\cdot{AD''}.\)
Mivel \(\displaystyle AD=f\), \(\displaystyle AD'=AB-BD\), illetve \(\displaystyle AD''=AC+CD\), előző eredményünkből \(\displaystyle f^2=({AB-BD})\cdot({AC+CD})\) következik, ez éppen a feladat állítása, hiszen ebből a nyilvánvalóan pozitív \(\displaystyle AB-BD\) és \(\displaystyle AC+CD\) számok mértani közepe:
\(\displaystyle f=\sqrt{(AB-BD)\cdot(AC+CD)}.\)
Megjegyzés. Könnyen bizonyítható, hogy a feladat állítása tetszőleges háromszögre igaz.
Statistics:
116 students sent a solution. 5 points: 60 students. 4 points: 11 students. 3 points: 7 students. 2 points: 9 students. 1 point: 6 students. 0 point: 8 students. Unfair, not evaluated: 1 solutions. Not shown because of missing birth date or parental permission: 1 solutions.
Problems in Mathematics of KöMaL, October 2021
