Problem C. 1690. (November 2021)

C. 1690. The centre of a semicircle of unit radius and diameter \(\displaystyle AB\) is \(\displaystyle O\). The semicircle of diameter \(\displaystyle OB\), centred at \(\displaystyle K\) is drawn inside the larger semicircle. A ray drawn from point \(\displaystyle A\) touches the small semicircle at point \(\displaystyle C\). The perpendicular dropped from point \(\displaystyle O\) to \(\displaystyle AC\) intersects the arc of diameter \(\displaystyle AB\) at a point \(\displaystyle D\). Prove that the midpoint of line segment \(\displaystyle BD\) is \(\displaystyle C\).

(5 pont)

Deadline expired on December 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Tekintsük az alábbi ábrát, amelyen az \(\displaystyle AC\)-re merőleges \(\displaystyle OD\) egyenes talppontját \(\displaystyle E\)-vel, az \(\displaystyle AC\) egyenesnek a nagyobbik félkörrel való metszéspontját \(\displaystyle F\)-fel jelöltük. A \(\displaystyle C\) pontot összekötöttük a kisebb félkör \(\displaystyle K\) középpontjával.

Az \(\displaystyle ABF\) és \(\displaystyle OBC\) háromszögek Thalész tétele miatt az \(\displaystyle F\), illetve \(\displaystyle C\) pontban derékszögű háromszögek. A két derékszögű háromszög körülírt körének sugara \(\displaystyle OA=OB=OD=1\), illetve \(\displaystyle KO=KB=KC=\frac{1}{2}\). Tudjuk, hogy a kisebb félkörben a \(\displaystyle KC\) sugár a \(\displaystyle C\) pontban merőleges a félkör \(\displaystyle AF\) érintőjére, és ezért \(\displaystyle OE\parallel{KC}\parallel{BF}\). Ez pedig azt jelenti, hogy \(\displaystyle OBFE\) derékszögű trapéz, amelynek \(\displaystyle KC\) a középvonala, és így egyrészt \(\displaystyle C\) felezi a trapéz \(\displaystyle EF\) szárát, másrészt \(\displaystyle KC=\frac{OE+BF}{2}\), azaz

\(\displaystyle 1=2KC=OE+BF.\)

Mivel \(\displaystyle OE+DE=1\) szintén igaz, ezért azt kapjuk, hogy \(\displaystyle DE=BF\). A \(\displaystyle CDE\) és \(\displaystyle CBF\) derékszögű háromszögekben tehát a \(\displaystyle DE\) és \(\displaystyle BF\), illetve \(\displaystyle CE\) és \(\displaystyle CF\) befogók egyenlők, ezért a két derékszögű háromszög egybevágó. Ekkor az átfogóik is egyenlő hosszúak, azaz \(\displaystyle BC=DC\). A két háromszög egybevágósága miatt \(\displaystyle BCF\sphericalangle=DCE\sphericalangle\), és ez csakis úgy lehetséges, ha a \(\displaystyle B,C\) és \(\displaystyle D\) pontok egy egyenesen vannak, és így a \(\displaystyle BD\) szakasz felezőpontja valóban \(\displaystyle C\).

2. megoldás. Az ehhez a megoldáshoz használt ábrán jelöléseink az előző megoldás ábrájának megfelelőek, az \(\displaystyle OBC\sphericalangle\)-et \(\displaystyle \beta\)-val jelöltük.

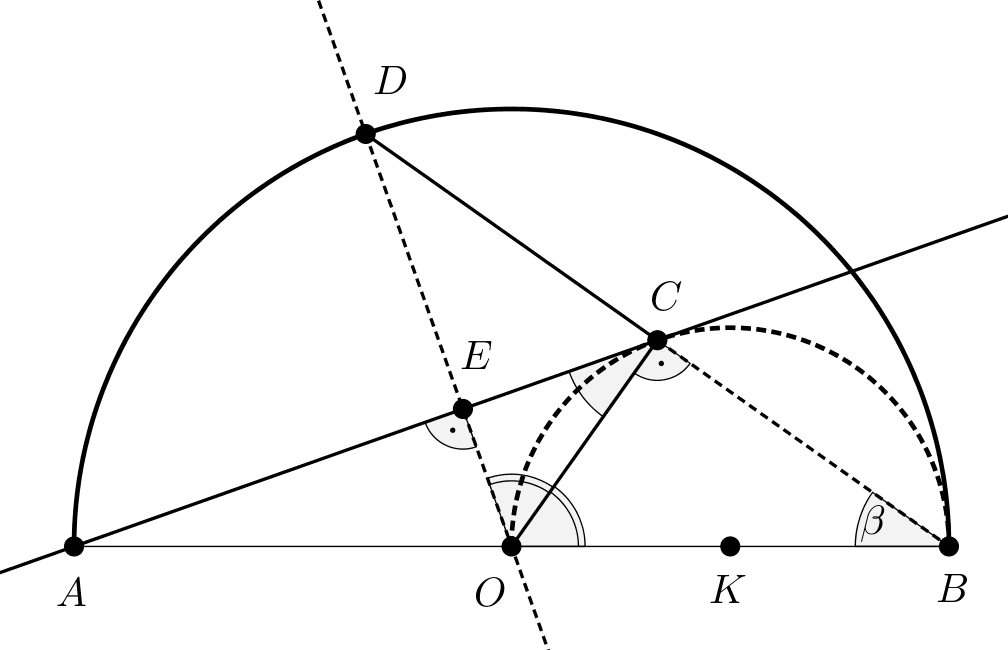
Thalész tétele miatt az \(\displaystyle OBC\) háromszög derékszögű, amelynek átfogója \(\displaystyle OB\).

Az \(\displaystyle OBC\) derékszögű háromszögben ezért \(\displaystyle COB\sphericalangle=90^{\circ}-\beta\).

Az \(\displaystyle AC\) egyenes érintője az \(\displaystyle OB\) átmérőjű félkörnek, emiatt az \(\displaystyle OCE\sphericalangle\) olyan, a félkörhöz rajzolt érintőszárú kerületi szög, amelyik az \(\displaystyle OC\) ívhez tartozik. Ehhez az ívhez tartozik a félkörben az \(\displaystyle OBC\sphericalangle=\beta\) kerületi szög, ez pedig a kerületi szögek tétele szerint azt jelenti, hogy \(\displaystyle OCE\sphericalangle=\beta\), és így \(\displaystyle COE\sphericalangle=90^{\circ}-\beta\).

Az \(\displaystyle OBC\) és \(\displaystyle ODC\) háromszögekben \(\displaystyle OB=OD=1\) az \(\displaystyle AB\) átmérőjű félkör sugara, illetve a két háromszögben közös az \(\displaystyle OC\) oldal, valamint a két-két megfelelő oldal által bezárt szögek is egyenlők, hiszen \(\displaystyle COB\sphericalangle=COD\sphericalangle=90^{\circ}-\beta\). Az \(\displaystyle OBC\) és \(\displaystyle ODC\) háromszögek tehát egybevágók, ezért a két háromszögben a harmadik oldalak is egyenlő hosszúak, vagyis \(\displaystyle BC=DC\).

Az egybevágóságból az is következik, hogy \(\displaystyle OCB\sphericalangle=OCD\sphericalangle=90^{\circ}\), azaz \(\displaystyle BCD\sphericalangle=180^{\circ}\), vagyis a \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontok egy egyenesre esnek, és \(\displaystyle BC=DC\) alapján a \(\displaystyle BD\) szakasz felezőpontja valóban \(\displaystyle C\).

Statistics:

163 students sent a solution.
5 points:	97 students.
4 points:	21 students.
3 points:	8 students.
2 points:	5 students.
1 point:	2 students.
0 point:	6 students.
Unfair, not evaluated:	9 solutionss.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, November 2021