 Problem C. 1705. (February 2022)
Problem C. 1705. (February 2022)
C. 1705. Given that a certain quadrilateral is a kite, it is cyclic and its sides are 42 and 56 units long, what is the distance between the centres of the inscribed and circumscribed circles?
Proposed by A. Siposs, Budapest
(5 pont)
Deadline expired on March 10, 2022.
Sorry, the solution is available only in Hungarian. Google translation
1. megoldás. A deltoid érintőnégyszög, mert a szemben levő oldalainak összege a tengelyes szimmetria miatt egyenlő. Ezért, ha a deltoid húrnégyszög is, akkor, mivel két szemben levő szöge egyenlő nagyságú, ezért ezek a szögek derékszögek. Legyen az \(\displaystyle ABCD\) deltoid szimmetriatengelye az \(\displaystyle AC\) átló, így a \(\displaystyle B\) és \(\displaystyle D\) csúcsoknál levő belső szögek \(\displaystyle 90^{\circ}\)-osak. Tekintsük a következő ábrát.
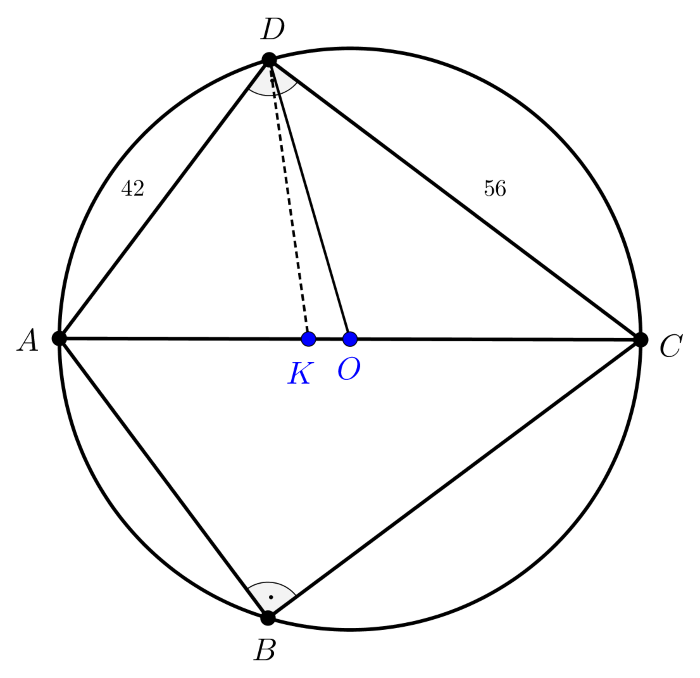
Az \(\displaystyle ABC\) és \(\displaystyle ADC\) derékszögű háromszögek, amelyeknek befogói a feltételek szerint \(\displaystyle AB=AD=42\) és \(\displaystyle BC=DC=56\).
A Pitagorasz-tételt alkalmazva \(\displaystyle 42^2+56^2={AC}^2\), ahonnan azt kapjuk, hogy \(\displaystyle AC=70\) hosszúságegység. A deltoid köré írt kör középpontja az \(\displaystyle AC\) átló \(\displaystyle O\) felezőpontja, így \(\displaystyle AO=35\).
Mivel a deltoid érintőnégyszög, ezért belső szögfelezői egy pontban metszik egymást. Az \(\displaystyle AC\) átló felezi az \(\displaystyle A\), illetve \(\displaystyle C\) csúcsnál levő belső szögeket, ezért a beírt kör középpontja az \(\displaystyle AC\) átlón van. Az ábrán megrajzoltuk a \(\displaystyle D\) csúcsnál levő derékszög szögfelezőjét, ez az átlót a beírt kör \(\displaystyle K\) középpontjában metszi.
Az \(\displaystyle ADC\) háromszögre felírjuk a belső szögfelező tételét:
\(\displaystyle \frac{AK}{70-AK}=\frac{42}{56},\)
innen egyszerű számolással kapjuk, hogy
\(\displaystyle 98AK=42\cdot70,\)
vagyis
\(\displaystyle AK=30.\)
Ebből azonnal következik \(\displaystyle AO=35\) alapján, hogy \(\displaystyle KO=5\), azaz a beírt és körülírt kör középpontja \(\displaystyle 5\) hosszúságegységre van egymástól.
2. megoldás. Felhasználjuk az 1. megoldás megállapításait és az ábra jelöléseit:
a \(\displaystyle B\) és \(\displaystyle D\) csúcsoknál levő belső szögek \(\displaystyle 90^{\circ}\)-osak, \(\displaystyle AC=70\), \(\displaystyle AO=35\), a beírt kör középpontja az \(\displaystyle AC\) átló \(\displaystyle K\) pontja.
Bocsássunk a \(\displaystyle K\) pontból merőlegeseket a \(\displaystyle CD\) és \(\displaystyle AD\) oldalakra, a merőlegesek talppontjai \(\displaystyle E\), illetve \(\displaystyle F\).
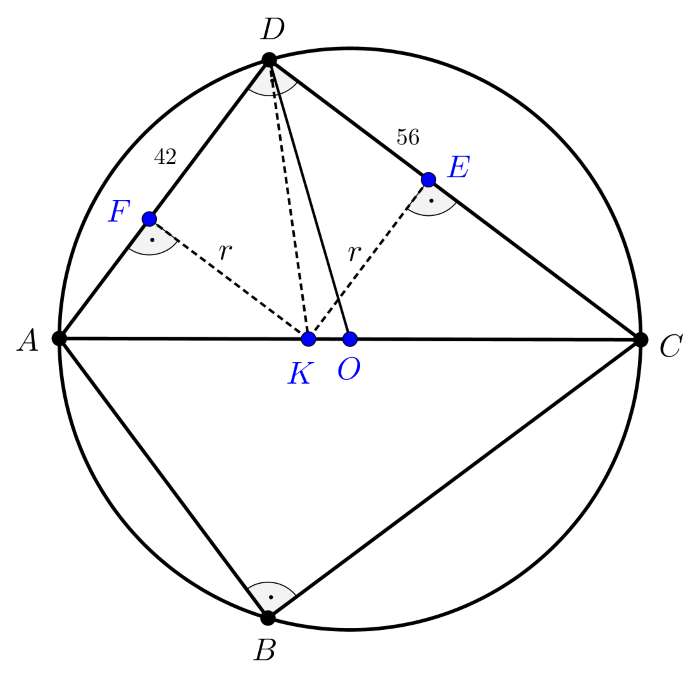
A \(\displaystyle KE\) és \(\displaystyle KF\) szakaszok hossza a beírt kör \(\displaystyle r\) sugara, a \(\displaystyle KEDF\) négyszög minden szöge derékszög, és \(\displaystyle KE=KF\) miatt a négyszög négyzet, tehát \(\displaystyle ED=FD=r\) is igaz.
Felhasználjuk azt a jól ismert összefüggést, hogy ha az \(\displaystyle ABCD\) érintőnégyszög területe \(\displaystyle t\), kerülete \(\displaystyle k\), akkor
| \(\displaystyle (1)\) | \(\displaystyle \frac{t}{k}=\frac{r}{2}.\) |
Az \(\displaystyle ABCD\) négyszög területe \(\displaystyle t=2\cdot{\frac{42\cdot56}{2}}=2352\) területegység, kerülete \(\displaystyle k=2\cdot(42+56)=196\) hosszúságegység, ennek megfelelően (1) alapján \(\displaystyle r=24\). Világos, hogy az \(\displaystyle AKF\) és \(\displaystyle ACD\) háromszögek hasonlók, hiszen megfelelő szögeik egyenlők az oldalak párhuzamossága, illetve egy egyenesre esése miatt.
A két háromszög megfelelő oldalainak aránya tehát egyenlő:
| \(\displaystyle (2)\) | \(\displaystyle \frac{r}{AK}=\frac{56}{AC}.\) |
Az \(\displaystyle r=24\) és \(\displaystyle AC=70\) behelyettesítése után (2)-ből adódik, hogy
\(\displaystyle AK=\frac{24\cdot70}{56}=30.\)
Ebből \(\displaystyle AO=35\) szerint következik, hogy \(\displaystyle KO=5\), ezért a beírt és körülírt kör középpontja \(\displaystyle 5\) hosszúságegységre van egymástól.
Megjegyzések. 1.) Az 1. megoldásban a szögfelezőtételből az is következik, hogy \(\displaystyle AK<CK\), tehát a \(\displaystyle K\) pont az ábrának megfelelően az \(\displaystyle AO\) szakasz belső pontja.
2.) Általánosan bizonyítható, hogy ha az \(\displaystyle ABCD\) deltoid húrnégyszög, szimmetriatengelye az \(\displaystyle AC\) átló, a négyszög oldalainak hossza \(\displaystyle a\) és \(\displaystyle b\), továbbá \(\displaystyle a<b\), akkor \(\displaystyle KO=\frac{((b-a)\sqrt{a^2+b^2}}{2(b+a)}\).
Ha \(\displaystyle b<a\), akkor az összefüggés számlálójában \(\displaystyle b-a\) helyett \(\displaystyle a-b\) szerepel, ha pedig \(\displaystyle a=b\), akkor a \(\displaystyle K\) és \(\displaystyle O\) pontok azonosak, vagyis \(\displaystyle KO=0\).
Statistics:
138 students sent a solution. 5 points: 100 students. 4 points: 7 students. 3 points: 4 students. 2 points: 3 students. 1 point: 1 student. 0 point: 2 students. Unfair, not evaluated: 4 solutionss. Not shown because of missing birth date or parental permission: 3 solutions.
Problems in Mathematics of KöMaL, February 2022
