 Problem C. 1712. (March 2022)
Problem C. 1712. (March 2022)
C. 1712. The sides of a pentagon are all equal in length, and two of its angles are right angles. What may be the measures of the other three angles?
Proposed by G. Károlyi, Budajenő
(5 pont)
Deadline expired on April 11, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelöljük az \(\displaystyle ABCDE\) ötszög oldalainak hosszát \(\displaystyle a\)-val. Az ötszög két derékszöge lehet két szomszédos csúcshoz, vagy két nem szomszédos csúcshoz tartozó belső szög.
Legyen először derékszög az \(\displaystyle A\) és \(\displaystyle B\) csúcsoknál. Mivel a feladat szövege nem írta elő, hogy a négyszög konvex, ezért az \(\displaystyle ABCD\) konkáv négyszög is lehet, a két esetet az 1. ábra szemlélteti.
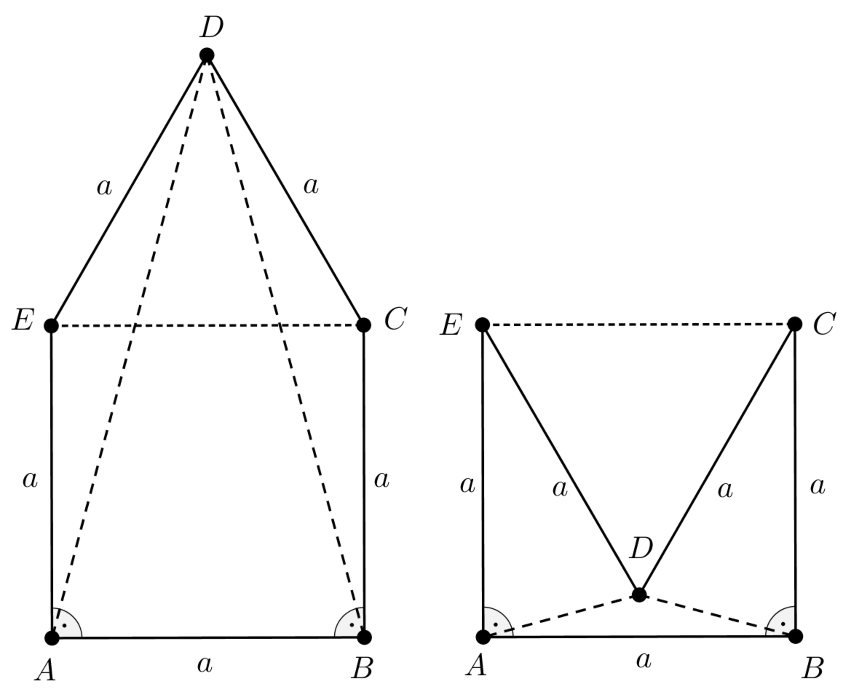
1. ábra
Mindkét esetre fennáll, hogy a két szomszédos csúcsnál levő derékszög és \(\displaystyle EA=AB=BC=a\) miatt az \(\displaystyle ABCE\) négyszög négyzet, ezért egyrészt \(\displaystyle EC=a\), másrészt \(\displaystyle BCE\sphericalangle=CEA\sphericalangle=90^{\circ}\). Az oldalak egyenlősége miatt a \(\displaystyle CDE\) háromszög mindkét esetben szabályos, így \(\displaystyle CDE\sphericalangle=DEC\sphericalangle=ECD\sphericalangle=60^{\circ}\).
Ebből azonnal következik, hogy az \(\displaystyle ABCDE\) ötszög ismeretlen szögei az 1. ábra első rajzán \(\displaystyle BCD\sphericalangle=DEA\sphericalangle=90^{\circ}+60^{\circ}=150^{\circ}\) és \(\displaystyle CDE\sphericalangle=60^{\circ}\), míg a második \(\displaystyle ABCDE\) négyszögben \(\displaystyle BCD\sphericalangle=DEA\sphericalangle=90^{\circ}-60^{\circ}=30^{\circ}\), a \(\displaystyle D\) csúcsnál pedig a \(\displaystyle CDE\sphericalangle=60^{\circ}\)-os szöget \(\displaystyle 360^{\circ}\)-ra kiegészítő, azaz \(\displaystyle 300^{\circ}\)-os belső szöget kapunk.
Ha a két derékszög két nem szomszédos csúcsnál helyezkedik el, akkor nem sérti az általánosságot, ha feltesszük, hogy a két derékszögű csúcs a \(\displaystyle C\) és az \(\displaystyle E\).
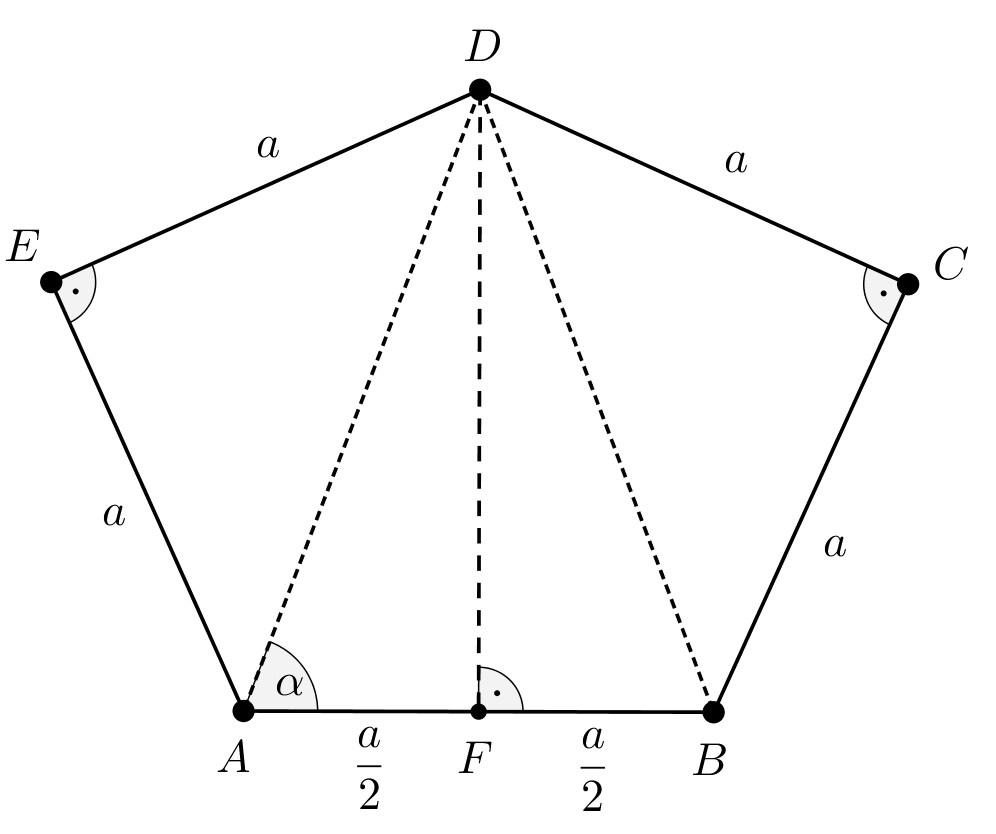
2. ábra
Konkáv négyszöget ezúttal is létrehozhatnánk, például úgy, hogy az \(\displaystyle ABC\) háromszöget a \(\displaystyle AC\)-re, vagy a \(\displaystyle BCD\) háromszöget a \(\displaystyle BD\)-re, vagy a \(\displaystyle CDE\) háromszöget a \(\displaystyle CE\)-re tükrözzük, az így kapott konkáv ötszögek mindegyikére teljesülni fog, hogy az oldalaik egyenlő hosszúak, de minden ilyen eset ellenkezne azzal a feltétellel, hogy az ötszögben a két szemben levő szög derékszög, mert a tükrözés legalább az egyik \(\displaystyle 90^{\circ}\)-os belső szöget megváltoztatná. Ezért ezúttal nem kapunk konkáv ötszöget.
A 2. ábrán a \(\displaystyle DE=AE=DC=BC=a\) feltétel és a derékszögek miatt \(\displaystyle ADE\) és \(\displaystyle BCD\) egyenlő szárú derékszögű háromszögek, ebből \(\displaystyle AD=BD=a\sqrt{2}\), illetve \(\displaystyle DAE\sphericalangle=ADE\sphericalangle=DBC\sphericalangle=BDC\sphericalangle=45^{\circ}\).
Az \(\displaystyle ABD\) egyenlő szárú háromszög \(\displaystyle AB\) oldalának felezőpontját \(\displaystyle F\)-fel jelöltük, a háromszög alapon fekvő szögei \(\displaystyle BAD\sphericalangle=ABD\sphericalangle=\alpha\).
Az \(\displaystyle AFD\) derékszögű háromszögben felírhatjuk, hogy \(\displaystyle \displaystyle{\cos{\alpha}=\frac{AF}{AD}=\frac{\frac{a}{2}}{a\sqrt{2}}=\frac{1}{2\sqrt{2}}}\). Ebből számológép segítségével azt kapjuk, hogy \(\displaystyle \alpha{\approx69,295^{\circ}}\) és emiatt \(\displaystyle ADF\sphericalangle\approx{20,705^{\circ}}\).
Az \(\displaystyle ABCDE\) ötszög ismeretlen szögei ebben az esetben \(\displaystyle EAB\sphericalangle=CBA\sphericalangle=\alpha+45^{\circ}\approx{114,295^{\circ}}\) és \(\displaystyle EDC\sphericalangle=2\cdot45^{\circ}+2\cdot{ADF\sphericalangle}\approx{131,41^{\circ}}\). Ezzel a feladatot megoldottuk.
Statistics:
39 students sent a solution. 5 points: Besze Zsolt, Cynolter Dorottya, Pekk Márton, Rumpler Bianka, Sipeki Márton, Szabó Zóra, Szegedi Ágoston, Tóth Gréta, Waldhauser Miklós. 4 points: Egyházi Hanna, Radzik Réka, Schneider Dávid, Szalanics Tamás, Werner Kinga. 3 points: 15 students. 2 points: 4 students. 1 point: 2 students. Unfair, not evaluated: 2 solutionss.
Problems in Mathematics of KöMaL, March 2022
